Question

（2010•百色）已知矩形ABCD中，对角线AC、BD相交于点O，E、F是对角线BD上的两点，且BF=DE．
（1）按边分类，△AOB是______三角形；
（2）猜想线段AE、CF的大小关系，并证明你的猜想．

Answer 1

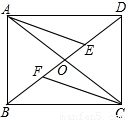
【答案】分析：（1）由于矩形的对角线相等且互相平分，可得OA=OB，因此从边的角度来看，△AOB是等腰三角形．
（2）此题的证法较多，以两种常见的证法为例：由矩形的性质，易得到OA=OC，OB=OC，进而可得到OF=OE，然后：
①通过证△AOE≌△COF来得到AE=CF；
②根据AC、EF互相平分判定四边形AFCE是平行四边形，从而得到AE=CF的结论．
解答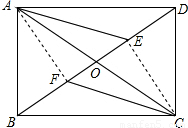：解：（1）等腰；
理由：由于矩形的对角线相等且互相平分，所以OA=OB，即△AOB是等腰三角形．

（2）猜想：AE=CF；
证法一：∵四边形ABCD是矩形，
∴AD∥BC，且AD=BC，
∴∠ADB=∠CBD，
∵DE=BF，
∴△ADE≌△CBF（SAS），
∴AE=CF．
证法二：∵四边形ABCD是矩形，
∴OA=OC，OB=OD，
∵DE=BF，∴OE=OF，
又∠AOE=∠COF，
∴△AOE≌△COF（SAS），
∴AE=CF．
证法三：如图，连接AF、CE，
由四边形ABCD是矩形得OA=OC，OB=OD，
∵DE=BF，∴OE=OF，
∴四边形AECF是平行四边形，
∴AE=CF．
点评：此题主要考查的是矩形的性质以及全等三角形的判定和性质，难度不大．