题目内容
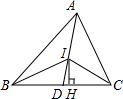 如图,已知三角形ABC的三个内角平分线交于点I,IH⊥BC于H,试比较∠CIH和∠BID的大小.
如图,已知三角形ABC的三个内角平分线交于点I,IH⊥BC于H,试比较∠CIH和∠BID的大小.
分析:根据角平分线的定义、三角形内角和定理可知∠BAD+∠ABI+∠HCI=90°.又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,所以∠BID=∠CIH.
解答:解:因为AI、BI、CI为三角形ABC的角平分线,
所以∠BAD=
∠BAC,
∠ABI=
∠ABC,
∠HCI=
∠ACB.
所以∠BAD+∠ABI+∠HCI
=
∠BAC+
∠ABC+
∠ACB
=
(∠BAC+∠ABC+∠ACB)
=
×180°
=90°.
所以∠BAD+∠ABI=90°-∠HCI.
又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,
2(∠BAD+∠ABI+∠HCI)=180°,
∠BAD+∠ABI+∠HCI=90°,
所以∠BID=∠CIH.
所以∠BID和∠CIH是相等的关系.
所以∠BAD=
| 1 |
| 2 |
∠ABI=
| 1 |
| 2 |
∠HCI=
| 1 |
| 2 |
所以∠BAD+∠ABI+∠HCI
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°.
所以∠BAD+∠ABI=90°-∠HCI.
又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,

2(∠BAD+∠ABI+∠HCI)=180°,
∠BAD+∠ABI+∠HCI=90°,
所以∠BID=∠CIH.
所以∠BID和∠CIH是相等的关系.
点评:本题考查了角平分线的定义及三角形内角和定理:三角形三个内角的和为180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 15、如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( )对.
15、如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( )对.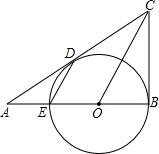 点E,与AC切于点D.
点E,与AC切于点D.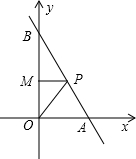 )是折线O→A→B上的动点(不与O点、B点重合),连接OP,MP,设△OPM的面积为S.
)是折线O→A→B上的动点(不与O点、B点重合),连接OP,MP,设△OPM的面积为S.
 按要求画图并填空:如图,已知三角形ABC及点D,CB⊥AB,B为垂足.
按要求画图并填空:如图,已知三角形ABC及点D,CB⊥AB,B为垂足.