题目内容
【题目】如图,直线l:y=2x+4
(1)①直接写出直线l关于y轴对称的直线l1的解析式_______.
②直接写出直线l向右平移2个单位得到的直线l2的解析式________.
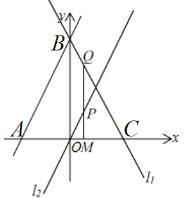
(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l1于点Q、交直线l2于点P.若PM=2PQ,求M点的坐标.
【答案】(1)①y=﹣2x+4;②y=2x;(2)M(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)①先求出点A,B坐标,再利用对称性求出点C坐标,最后利用待定系数法即可得出结论;
②利用平移的性质即可得出结论;
(2)设出点M坐标,进而表示出点P,Q坐标,即可表示出PM,PQ,最后建立方程求解即可得出结论.
解:①如图,记直线y=2x+4与y轴的交点为A,与x轴的交点为B,
∴A(﹣2,0),B(0,4),
∴点A关于y轴的对称点C的坐标为(2,0),
设直线l1的解析式的解析式为y=kx+4,
∴2k+4=0,
∴k=﹣2,
∴直线l1的解析式y=﹣2x+4;
②直线l:y=2x+4向右平移2个单位得到的直线l2的解析式y=2(x﹣2)+4=2x,
故答案为:y=﹣2x+4,y=2x;
(2)如图,
设点M(m,0),
∵点P在直线l2:y=2x上,
∴P(m,2m),
∵点Q在直线l1:y=﹣2x+4上,
∴Q(m,﹣2m+4),
∴PM=|2m|,PQ=|2m﹣(﹣2m+4)|=4|m﹣1|,
∵PM=2PQ,
∴|2m|=2×4|m﹣1|,
∴m=![]() 或m=
或m=![]() ,
,
∴M(![]() ,0)或(
,0)或(![]() ,0).
,0).

【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?