题目内容
 如图,Rt△ACB的点A在坐标原点,点C在x轴上.将Rt△ACB沿x轴方向向右平移3个单位得到Rt△EFD.点D的坐标为(5,4).双曲线
如图,Rt△ACB的点A在坐标原点,点C在x轴上.将Rt△ACB沿x轴方向向右平移3个单位得到Rt△EFD.点D的坐标为(5,4).双曲线 过点B且交DF于点M.
过点B且交DF于点M.
(1)求k的值.
(2)求△BDM的面积.
解:(1)依题意,点B沿x轴方向向右平移3个单位得到点D(5,4),
所以,B(2,4),
将B点坐标代入双曲线 中,得k=xy=8;
中,得k=xy=8;
(2)∵DM⊥x轴,
∴M点横坐标为5,纵坐标y=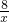 =
= ,
,
∴DM=4- =
= ,BD=5-2=3,
,BD=5-2=3,
∴S△BDM= ×BD×DM=
×BD×DM= ×3×
×3× =
=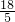 .
.
分析:(1)已知D(5,4),由平移可知B(2,4),将B点坐标代入双曲线 中可求k的值;
中可求k的值;
(2)已知DM⊥x轴,则M点横坐标与D点横坐标都是5,根据M点的横坐标可求纵坐标,再求线段DM,BD的长,求△BDM的面积.
点评:本题考查了反比例函数的综合运用.关键是由平行于x轴的直线上的点纵坐标相等,垂直于x轴的直线上的点横坐标相等,以及平移的性质求相关点的坐标.
所以,B(2,4),
将B点坐标代入双曲线
 中,得k=xy=8;
中,得k=xy=8;(2)∵DM⊥x轴,
∴M点横坐标为5,纵坐标y=
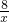 =
= ,
,∴DM=4-
 =
= ,BD=5-2=3,
,BD=5-2=3,∴S△BDM=
 ×BD×DM=
×BD×DM= ×3×
×3× =
=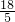 .
.分析:(1)已知D(5,4),由平移可知B(2,4),将B点坐标代入双曲线
 中可求k的值;
中可求k的值;(2)已知DM⊥x轴,则M点横坐标与D点横坐标都是5,根据M点的横坐标可求纵坐标,再求线段DM,BD的长,求△BDM的面积.
点评:本题考查了反比例函数的综合运用.关键是由平行于x轴的直线上的点纵坐标相等,垂直于x轴的直线上的点横坐标相等,以及平移的性质求相关点的坐标.

练习册系列答案
相关题目
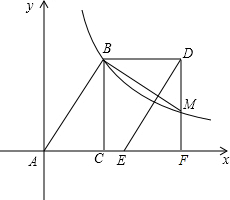 (2012•长春一模)如图,Rt△ACB的点A在坐标原点,点C在x轴上.将Rt△ACB沿x轴方向向右平移3个单位得到Rt△EFD.点D的坐标为(5,4).双曲线
(2012•长春一模)如图,Rt△ACB的点A在坐标原点,点C在x轴上.将Rt△ACB沿x轴方向向右平移3个单位得到Rt△EFD.点D的坐标为(5,4).双曲线 如图,Rt△ACB的斜边AB=4cm,一条直角边AC=2cm,如果以直线BC为轴旋转一周后得到一个圆锥,则这个圆锥的侧面积为
如图,Rt△ACB的斜边AB=4cm,一条直角边AC=2cm,如果以直线BC为轴旋转一周后得到一个圆锥,则这个圆锥的侧面积为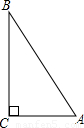
 如图,Rt△ACB的点A在坐标原点,点C在x轴上.将Rt△ACB沿x轴方向向右平移3个单位得到Rt△EFD.点D的坐标为(5,4).双曲线
如图,Rt△ACB的点A在坐标原点,点C在x轴上.将Rt△ACB沿x轴方向向右平移3个单位得到Rt△EFD.点D的坐标为(5,4).双曲线 过点B且交DF于点M.
过点B且交DF于点M.