题目内容
如图1,正方形OCDE的边长为1,阴影部分的面积记作S1;如图2,最大圆半径r=1,阴影部分的面积记作S2,则S1 S2(用“>”、“<”或“=”填空).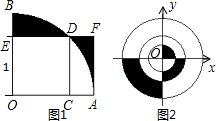

<。
结合图形发现:图1阴影部分的面积等于等于矩形ACDF的面积,图2每个阴影部分正好是它所在的圆的四分之一,则阴影部分的面积大圆面积的四分之一。计算出结果后再比较S1与S2的大小即可:
∵正方形OCDE的边长为1,∴根据勾股定理得OD=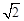 , ∴AO=
, ∴AO=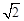 。
。
∴AC=AO-CO=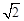 -1。∴
-1。∴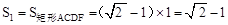 。
。
∵大圆面积=πr2=π∴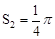 。
。
∵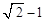 <
<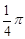 ,∴S1<S2。
,∴S1<S2。
∵正方形OCDE的边长为1,∴根据勾股定理得OD=
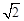 , ∴AO=
, ∴AO=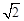 。
。∴AC=AO-CO=
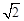 -1。∴
-1。∴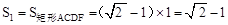 。
。∵大圆面积=πr2=π∴
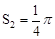 。
。∵
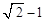 <
<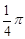 ,∴S1<S2。
,∴S1<S2。
练习册系列答案
相关题目
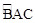 的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。
的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。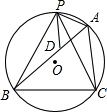
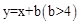 与x轴、y轴分别相交于点A、B,与正比例函数
与x轴、y轴分别相交于点A、B,与正比例函数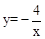 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。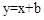 与⊙O有哪些位置关系?求出相应b的取值范围。
与⊙O有哪些位置关系?求出相应b的取值范围。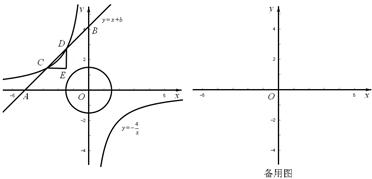
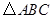 中,
中,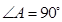 ,
,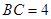 cm,分别以B、C为圆心的两个等圆外切,则图中阴影部分的面积为
cm,分别以B、C为圆心的两个等圆外切,则图中阴影部分的面积为 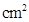 .
.