题目内容
(1999•北京)如果在数轴上表示a,b两个实数的点的位置如图所示,那么|a-b|+|a+b|化简的结果为( )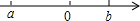
A.2a
B.-2a
C.0
D.2b
【答案】分析:先由数轴上a,b的位置判断出其符号,再根据其与原点的距离判断出a,b绝对值的大小,代入原式求值即可.
解答:解:由数轴可a<0,b>0,a<b,|a|>b,
所以a-b<0,a+b<0,∴|a-b|+|a+b|=-a+b-a-b=-2a.
故选B.
点评:此题主要考查了绝对值的定义,即正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值还是0.除此之外还考查了数轴的概念和整式的加减.
解答:解:由数轴可a<0,b>0,a<b,|a|>b,
所以a-b<0,a+b<0,∴|a-b|+|a+b|=-a+b-a-b=-2a.
故选B.
点评:此题主要考查了绝对值的定义,即正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值还是0.除此之外还考查了数轴的概念和整式的加减.

练习册系列答案
相关题目
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.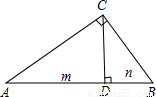
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.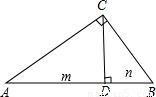
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
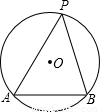
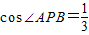 ,问是否存在以A、P、B为顶点的面积最大的三角形?试说明理由;若存在,求出这个三角形的面积.
,问是否存在以A、P、B为顶点的面积最大的三角形?试说明理由;若存在,求出这个三角形的面积.