题目内容
(1999•北京)如图,已知△ABC中,∠ACB=90°,过C点作CD⊥AB,垂足为D,且AD=m,BD=n,AC2:BC2=2:1,又关于x的方程 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
【答案】分析:根据△ABC∽△ACD,求出m和n之间的关系式;再根据根与系数的关系求出m、n的取值范围,然后估算,即可求得一次函数的解析式.
解答:解:易证△ABC∽△ACD,∴ =
=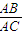 ,AC2=AD•AB,同理BC2=BD•AB,
,AC2=AD•AB,同理BC2=BD•AB,
∴ =
= ,∵
,∵ =
= ,∴
,∴ =
= ,∴m=2n…①,
,∴m=2n…①,
∵关于x的方程 x2-2(n-1)x+m2-12=0有两实数根,
x2-2(n-1)x+m2-12=0有两实数根,
∴△=[-2(n-1)]2-4× ×(m2-12)≥0,
×(m2-12)≥0,
∴4n2-m2-8n+16≥0,把①代入上式得n≤2…②,
设关于x的方程 x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,
x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,
则x1+x2=8(n-1),x1•x2=4(m2-2),
依题意有(x1-x2)2<192,即[8(n-1)]2-16(m2-12)<192,
∴4n2-m2-8n+4<0,把①式代入上式得n> …③,由②、③得
…③,由②、③得 <n≤2,
<n≤2,
∵m、n为整数,∴n的整数值为1,2,
当n=1,m=2时,所求解析式为y=2x+1,当n=2,m=4时,解析式为y=4x+2.
点评:此题结合了相似三角形和根的判别式,还要对整数值进行估算,难度较大,有利于培养同学们钻研和探索问题的能力.
解答:解:易证△ABC∽△ACD,∴
 =
=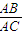 ,AC2=AD•AB,同理BC2=BD•AB,
,AC2=AD•AB,同理BC2=BD•AB,∴
 =
= ,∵
,∵ =
= ,∴
,∴ =
= ,∴m=2n…①,
,∴m=2n…①,∵关于x的方程
 x2-2(n-1)x+m2-12=0有两实数根,
x2-2(n-1)x+m2-12=0有两实数根,∴△=[-2(n-1)]2-4×
 ×(m2-12)≥0,
×(m2-12)≥0,∴4n2-m2-8n+16≥0,把①代入上式得n≤2…②,
设关于x的方程
 x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,
x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,则x1+x2=8(n-1),x1•x2=4(m2-2),
依题意有(x1-x2)2<192,即[8(n-1)]2-16(m2-12)<192,
∴4n2-m2-8n+4<0,把①式代入上式得n>
 …③,由②、③得
…③,由②、③得 <n≤2,
<n≤2,∵m、n为整数,∴n的整数值为1,2,
当n=1,m=2时,所求解析式为y=2x+1,当n=2,m=4时,解析式为y=4x+2.
点评:此题结合了相似三角形和根的判别式,还要对整数值进行估算,难度较大,有利于培养同学们钻研和探索问题的能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.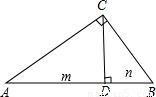
 x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
x2-2(n-1)x+m2-12=0两实数根的差的平方小于192,求:m,n为整数时,一次函数y=mx+n的解析式.
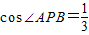 ,问是否存在以A、P、B为顶点的面积最大的三角形?试说明理由;若存在,求出这个三角形的面积.
,问是否存在以A、P、B为顶点的面积最大的三角形?试说明理由;若存在,求出这个三角形的面积.