Question

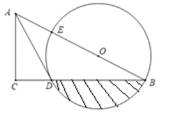
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D为AB边上一点，且AD＝1，点P从点C出发，沿射线CA以每秒1个单位长度的速度运动，以CP、DP为邻边作CPDE．设CPDE和△ABC重叠部分图形的面积为S（平方单位），点P的运动时间为t（秒）（t＞0）

（1）连结CD，求CD的长；

（2）当CPDE为菱形时，求t的值；

（3）求S与t之间的函数关系式；

（4）将线段CD沿直线CE翻折得到线段C′D′．当点D′落在△ABC的边上时，直接写出t的值．

Answer 1

【答案】（1）CD=；（2）t＝；（3）S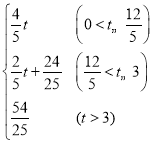＝；（4）满足条件的t的值为s或s．

【解析】

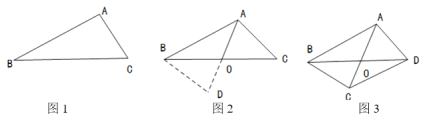
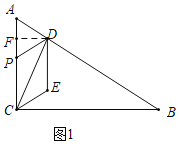
（1）过点D作DF⊥AC于点F．如图1中．求出DF，CF，利用勾股定理即可解决问题．

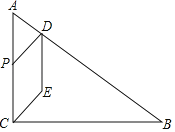
（2）当为菱形时，如图2中，连接BP交CD于O．证明△COP∽△BCP，推出=，由此构建方程即可解决问题．

（3）分三种情形：当0<t≤时，如图3中，重叠部分是四边形PCED．当<t≤3时，如图4中，重叠部分是四边形PCFD．当t>3时，如图 5中，重叠部分是四边形ACFD，分别求解即可解决问题．

（4）分两种情形分别画出图形求解即可．

解：（1）过点D作DF⊥AC于点F．如图1．

在Rt△ABC中，∠ACB=90°，

∴AB===5，

∵DF∥BC，

∴△AFD∽△ACB．

∴==，

∴==，

∴AF=，DF=，

∴CF=AC﹣AF=3﹣=，

在Rt△CDF中，∠CFD=90°，

∴CD===．

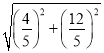（2）当为菱形时，如图2中，连接BP交CD于O．

∵四边形PCED是菱形，

∴PD=PC，

∵BD=BC=1，

∴PB垂直平分线段CD，

∴点E在直线PB上，

∵∠CPO+∠PCO=90°，∠CPB+∠PBC=90°，

∴∠PCO=∠PBC，∵∠POC=∠PCB，

∴△COP∽△BCP，

∴=，

∴=．

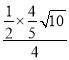∴t=．

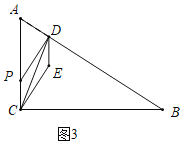
（3）当0<t≤时，如图3中，重叠部分是四边形PCED．

．

S=t=t．

当<t≤3时，如图4中，重叠部分是四边形PCFD．

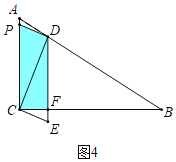
S=(4×+t)﹣=t+．

当t>3时，如图 5中，重叠部分是四边形ACFD，

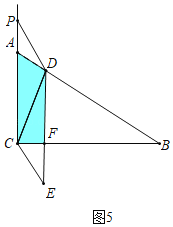
S=(4×+3)﹣=．

综上所述，S=．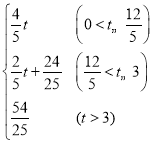

（4）如图6中，当点D′落在AB上时，延长CE交AB于O，

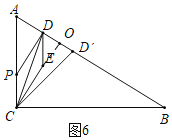
易知OC⊥AB，OC=．AO=，

∴OD=OA﹣AD=，

∵DE∥AC，

∴=，

∴=，

∴DE=，

此时t=，

如图7中，当点D′落在BC上时，延长DE交BC于F，作OM⊥BC于M，ON⊥CD于N．

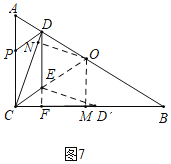
∵∠DCO=∠OCB，ON⊥CD，OM⊥CB，

∴ON=OM，

∵S△DCB=S△CDO+S△BCO，

∴×4×=××ON+×4×OM，

∴OM=，

∵OM∥AC，

∴=，

∴BM=，CM=，

∵EF∥OM，

∴=，可得EF=，

∴CP=DE=﹣=，

此时t=，

综上所述，满足条件的t的值为s或s．