题目内容
【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
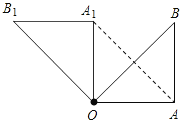
(1)线段OA1的长是 ,∠AOB1的度数是 ;
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
【答案】(1)6,135°;(2)证明见解析;(3)OAA1B1的面积36.
【解析】
试题分析:(1)图形在旋转过程中,边长和角的度数不变;
(2)可证明OA∥A1B1且相等,即可证明四边形OAA1B1是平行四边形;
(3)平行四边形的面积=底×高=OA×OA1.
(1)解:因为,∠OAB=90°,OA=AB,
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°.
(2)证明:∵∠AOA1=∠OA1B1=90°,
∴OA∥A1B1,
又∵OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
(3)解:OAA1B1的面积=6×6=36.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目