题目内容
【题目】如图,反比例函数y= ![]() (x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则
(x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则 ![]() = , 当k=4时,四边形ODBE的面积为平方单位.
= , 当k=4时,四边形ODBE的面积为平方单位. 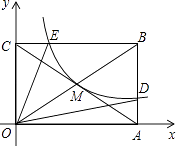
【答案】![]() ;12
;12
【解析】解:设B(a,b), ∴E( ![]() ,b),D(a,
,b),D(a, ![]() ),M(
),M( ![]() a,
a, ![]() b),
b),
∴k= ![]() a
a ![]() b=
b= ![]() ,
,
∴ab=4k,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
∵E、M、D位于反比例函数图象上,
则S△OCE= ![]() =2,S△OAD=
=2,S△OAD= ![]() =2,
=2,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=k,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4k=16,
∴2+2+S四边形ODBE=16,
解得:S四边形ODBE=12.
所以答案是 ![]() ;12.
;12.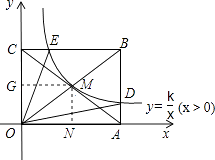
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
【题目】某销售公司为了提高员工的工作积极性,对员工的工资结构进行改革,改革后月工资由基本保障工资与计件奖励工资组成.(计件奖励工资=销售每件的奖励金额×销售的件数)下表是甲、乙两位职工今年三月份的工资情况信息:
职工 | 甲 | 乙 |
月销售件数(件) | 100 | 80 |
月工资(元) | 4500 | 4100 |
求员工的月基本保障工资和销售每件产品的奖励金额各多少元?