题目内容
【题目】已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.
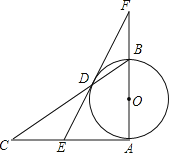
(1)求证:DE为⊙O的切线.
(2)求证:DF2=BFAF.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)连AD,OD,则∠ADB=∠ADC=90°,由直角三角形斜边上的中线性质得:EA=ED,∠EDA=∠EAD,由等腰三角形的性质得:∠ODA=∠OAD,证得∠EDO=∠EAO,即可得出结论;
(2)证明:由切线的性质得:∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,证出∠FDB=∠FAD,∠F为公共角,得出△FDB∽△FAD,由对应边成比例即可得出结论.
(1)证明:连AD,OD,如图所示:
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵E是AC的中点,
∴EA=ED,
∴∠EDA=∠EAD,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠EDO=∠EAO,
∵AB⊥AC,
∴∠EAO=90°,
∴∠EDO=90°,
∴DE为⊙O的切线;
(2)证明:∵DE为⊙O的切线,
∴∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠FDB=∠FAD,
又∵∠F为公共角,
∴△FDB∽△FAD,
∴![]() =
=![]() ,
,
∴DF2=BFAF.


练习册系列答案
相关题目
【题目】汽车刹车后,还会继续向前滑行一段距离,这段距离称为“刹车距离”刹车距离y(m)与刹车时的车速x(km/h)的部分关系如表:
刹车时的车速 | 0 | 50 | 100 | 200 |
刹车距离 | 0 | 5.5 | 46.5 | 82 |
(1)求出y与x之间的函数关系式.
(2)一辆车在限速120km/h的高速公路上行驶时出了事故,事后测得它的刹车距离为40.6m,问:该车在发生事故时是否超速行驶?