题目内容
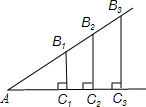观察图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3，易知Rt△AB1C1∽Rt△| B1C1 | AC1 |
分析：根据相似三角形的判定定理（AA）知，Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3，由相似三角形的对应边成比例填空即可．
解答：解：∵∠A=∠A=∠A，∠AC1B1=∠AC2B2=∠AC3B3=90°，
∴Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3（AA）；
∴
=
=
（相似三角形的对应边成比例）；
∵tan∠A=
=
=
．
故答案是：AB2C2、AB3C3、
、
．
∴Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3（AA）；
∴
| B1C1 |
| AC1 |
| B2C2 |
| AC2 |
| B3C3 |
| AC3 |
∵tan∠A=
| B1C1 |
| AC1 |
| B2C2 |
| AC2 |
| B3C3 |
| AC3 |
故答案是：AB2C2、AB3C3、
| B2C2 |
| AC2 |
| B3C3 |
| AC3 |
点评：本题考查了相似三角形的判定与性质．解答本题时，利用了相似三角形的判定定理AA和相似三角形的性质：对应边成比例．
练习册系列答案
阅读快车系列答案
相关题目
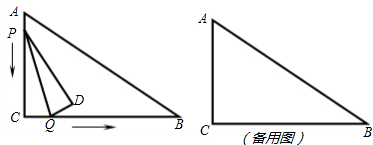
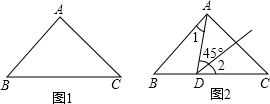
在Rt△ABC中，∠BAC=90°，AB=AC=4cm，实验操作：把一等腰直角三角尺45°角的顶点（记为点D），放在BC边上滑动（不与B，C重合），让该角的一边始终过点A，另一边交AC于点E，选取运动过程中的两个瞬间，用量角器分别测出∠BDA与∠CED的大小，并填入下表：
探索：（1）观察实验结果，猜想∠BDA与∠CED的大小有何关系？并证明你的结论；
（2）设BD=x，AE=y，试求出y关于x的函数关系式，并写出自变量x的取值范围；
（3）当点D在BC边上滑动时，△ADE能否成为等腰三角形？若能，求出点D的位置；若不能，请说明理由．（图1供实验操作用，图2备用）
| ∠BDA | ∠CED | |
| 第一次测量结果 | ||
| 第二次测量结果 |
（2）设BD=x，AE=y，试求出y关于x的函数关系式，并写出自变量x的取值范围；
（3）当点D在BC边上滑动时，△ADE能否成为等腰三角形？若能，求出点D的位置；若不能，请说明理由．（图1供实验操作用，图2备用）
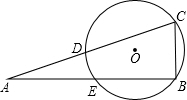交于另一点E．
