ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃКЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌгыyжсНЛгкЕуCЃЌЖдГЦжсЪЧжБЯпx=1ЃЌЧвЭМЯѓЯђгвЦНвЦвЛИіЕЅЮЛКѓОЙ§зјБъдЕуO,
ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌгыyжсНЛгкЕуCЃЌЖдГЦжсЪЧжБЯпx=1ЃЌЧвЭМЯѓЯђгвЦНвЦвЛИіЕЅЮЛКѓОЙ§зјБъдЕуO,
(1)ЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)жБЯп![]() НЛyжсгкDЕуЃЌEЮЊХзЮяЯпЖЅЕу.ШєЁЯDBC=ІСЃЌЁЯCBE=ІТЃЌЧѓІС-ІТЕФжЕ.
НЛyжсгкDЕуЃЌEЮЊХзЮяЯпЖЅЕу.ШєЁЯDBC=ІСЃЌЁЯCBE=ІТЃЌЧѓІС-ІТЕФжЕ.
(3)дк(2)ЮЪЕФЧАЬсЯТЃЌPЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЧвТњзуPA=PCЃЌдкyжсгвВрЕФХзЮяЯпЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУЁїBDMЕФУцЛ§ЕШгкPA2ШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.


ЁОД№АИЁПЃЈ1ЃЉетИіЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉІС-ІТ=45Ёу
ЃЈ3ЃЉзлЩЯЫљЪіЃЌДцдкЗћКЯЬѕМўЕФЕуMЦфзјБъЮЊ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁПЗжЮіЃК (1)ИљОнЖўДЮКЏЪ§ЕФЖдГЦадПЩЧѓЕУЕуBЕФзјБъЃЌНЋЫќУЧДњШыХзЮяЯпЕФНтЮіЪНжаЃЌЭЈЙ§СЊСЂЗНГЬзщЧѓЕУД§ЖЈЯЕЪ§ЕФжЕЃЌМДПЩШЗЖЈИУХзЮяЯпЕФНтЮіЪНЃЛ
(2)ИљОнХзЮяЯпКЭжБЯпBDЕФНтЮіЪНЃЌПЩЧѓЕУCЁЂDЁЂEЕФзјБъЃЌМДПЩЕУЕНЁЯOBC=ЁЯOCB=45 ЁуЃЛЫљЧѓНЧЕФЖШЪ§ВюПЩзЊЛЏЮЊЁЯOBCЕФЖШЪ§ЃЛдкRtЁїOBCжаЃЌвбОЧѓЕУЁЯOBC=ЁЯOCB=45 ЁуЃЌгЩДЫЕУНтЃЛ
(3)взжЊХзЮяЯпЕФЖдГЦжсЗНГЬЃЌПЩЩшГіЕуPЕФНтЮіЪНЃЌЧѓГіЕуPЕФзјБъЃЌНјЖјЕУЕНPAЕФжЕЃЌМДПЩЧѓЕУЁїBDMЕФУцЛ§ЃЎПЩгУУцЛ§ИюВЙЗЈЧѓНт.
БОЬтНтЮіЃК
(1)гЩЬтвтЃЌA(-1,0)
![]() ЖдГЦжсЪЧжБЯпx=1
ЖдГЦжсЪЧжБЯпx=1
ЁрB(3,0)
АбA(-1,0)ЃЌB(3,0)ЗжБ№ДњШыy=ax-2x+cЕУ![]()
НтЕУ![]()
ЁретИіЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=x-2x-3
(2) ЁпжБЯп![]() гыyжсНЛгкD(0,1), ЁрOD=1
гыyжсНЛгкD(0,1), ЁрOD=1
гЩY=X-2X-3=(x-1)-4ЕУE91ЃЌ-4ЃЉ
СЌНгCEЙ§EзїEFЁЭyжсгкF(ШчЭМ1)ЃЌдђEF=1
ЁпХзЮяЯпy=x-2x-3гыyжсНЛгкC90ЃЌ-3
ЁрOC=OB=3ЃЌCF=1=EF
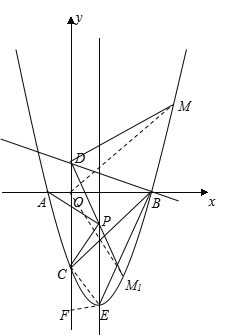
(ШчЭМ1)
ЁрЁЯOBC=ЁЯOCB=ЁЯFCE=45Ёу,
BC=![]() ,CE=
,CE=![]()
ЁрЁЯBCE=90Ёу=ЁЯBOD, ![]() ,
,
![]()
![]() Ёр
Ёр![]()
ЁрЁїBODЁзЁїBCE
ЁрЁЯCBF=ЁЯDBO
Ёр![]()
(3)ЩшP(1ЃЌn)
ЁпPA=PC
ЁрPA=PC, МД(1+1)+(n-0)=(1+0)+(n+3)
НтЕУn=-1
ЁрPA=(1+1)+(-1-0)=5
Ёр![]()
ЗНЗЈвЛЃКЩшДцдкЗћКЯЬѕМўЕФЕуM(m,m-2m-3),дђm>0
ЂйЕБMдкжБЯпBDЩЯВрЪБЃЌСЌНгOM(ШчЭМ1)ЃЌ
дђ![]()
МД![]()
![]()
ећРэЃЌЕУ![]()
НтЕУ![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ ![]()
Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
Ёр![]()
ЂкЕБMдкжБЯпBDЯТВрЪБЃЌВЛЗСНа![]() СЌНг
СЌНг![]() (ШчЭМ1)ЃЌ
(ШчЭМ1)ЃЌ
дђ![]()
МД![]()
![]()
ећРэЃЌЕУ![]()
НтЕУ![]() (ЩсШЅ)
(ЩсШЅ)
Абm=2ДњШы![]() ЕУy=-3
ЕУy=-3
Ёр![]()
злЩЯЫљЪіЃЌДцдкЗћКЯЬѕМўЕФЕуMЦфзјБъЮЊ![]() Лђ(2,-3).
Лђ(2,-3).
ЗНЗЈЖўЃКЩшДцдкЗћКЯЬѕМўЕФЕу![]() ЃЌдђm>0
ЃЌдђm>0

ЂйЕБMдкжБЯпBDЩЯВрЪБЃЌЙ§MзїMGЁЮyжсЃЌНЛDBгкG(ШчЭМ2)
ЩшDЁЂBЕНMGОрРыЗжБ№ЮЊ![]() дђ
дђ
![]()
МД![]() ,
, ![]() ,
,
![]()
ећРэЃЌЕУ![]()
НтЕУ![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ ![]()
Аб![]() ДњШыy=m-2m-3ЕУy=
ДњШыy=m-2m-3ЕУy=![]()
ЁрM(![]() )
)
ЂкЕБMдкжБЯпBDЯТВрЪБЃЌВЛЗСНаЙ§![]() зї
зї![]() ЁЮyжсЃЌНЛDBгк
ЁЮyжсЃЌНЛDBгк![]() (ШчЭМ2)
(ШчЭМ2)
ЩшDЁЂBЕН![]() ОрРыЗжБ№ЮЊ
ОрРыЗжБ№ЮЊ![]() дђ
дђ![]()
МД![]()
![]()
![]()
ећРэЃЌЕУ3m-5m-2=0
НтЕУ![]() (ЩсШЅ)
(ЩсШЅ)
Абm=2ДњШыy=m-2m-3ЕУy=-3
Ёр![]()
злЩЯЫљЪіЃЌДцдкЗћКЯЬѕМўЕФЕуMЦфзјБъЮЊ![]() Лђ(2,-3)
Лђ(2,-3)
ЗНЗЈШ§ЃКЂйЕБMдкжБЯпBDЩЯВрЪБЃЌЙ§MзїMHЁЮBDНЛyжсгкH,СЌНгBH(ШчЭМ3)
дђ![]() ,МД
,МД![]()
![]() ЁрDH=
ЁрDH=![]()
ЁрH(0, ![]() )
)
ЁржБЯпBHНтЮіЪНЮЊy=![]()
СЊСЂ ЕУ
ЕУ![]() Лђ
Лђ
![]() MдкyжсгвВр, ЁрMзјБъЮЊ
MдкyжсгвВр, ЁрMзјБъЮЊ![]()
ЂкЕБMдкжБЯпBDЯТВрЪБЃЌВЛЗСНа![]() Й§
Й§![]() зї
зї![]() ЁЮBDЃЌНЛyжсгк
ЁЮBDЃЌНЛyжсгк![]() ,
,
СЌНгB![]() (ШчЭМ3)ЃЌЭЌРэПЩЕУD
(ШчЭМ3)ЃЌЭЌРэПЩЕУD![]() =
=![]()
Ёр![]() (0,
(0, ![]() )
)
ЁржБЯп![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]()
СЊСЂ ЕУ
ЕУ![]() Лђ
Лђ
Ёп![]() дкyжсгвВрЃЌЁр
дкyжсгвВрЃЌЁр![]() зјБъЮЊ(2,-3)
зјБъЮЊ(2,-3)
злЩЯЫљЪіЃЌДцдкЗћКЯЬѕМўЕФЕуM,ЦфзјБъЮЊ![]() Лђ(2,-3).
Лђ(2,-3).

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ

