题目内容
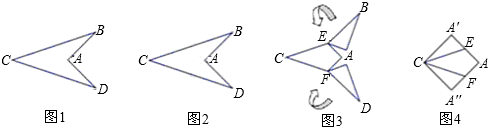
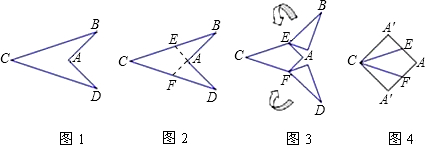
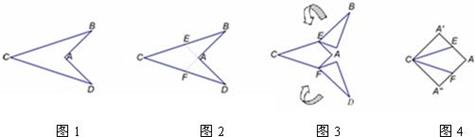
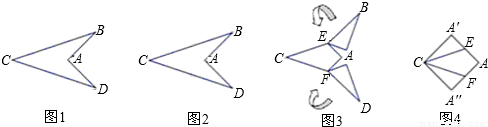
图1中的“箭头”是以AC所在直线为对称轴的轴对称图形,∠BAD=90°,AB=4.图2到图4是将“箭头”沿虚线剪拼成正方形的过程,求图1中BC的长.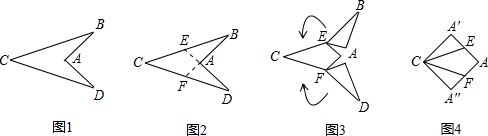

分析:根据剪拼,AE=AE′,根据正方形的四条边都相等可得AB=AA′,从而得到AA′=2AE,然后利用勾股定理列式求出BE,再根据BC=2BE代入数据计算即可得解.
解答:解:由题意可得,AB、2AE都是正方形边长,
AB=AA′=2AE,
∵AB=4,
∴AE=
×4=2,
在Rt△ABE中,BE=
=
=2
,
∴BC=2BE=4
.
AB=AA′=2AE,
∵AB=4,
∴AE=
| 1 |
| 2 |
在Rt△ABE中,BE=
| AB2+AE2 |
| 42+22 |
| 5 |
∴BC=2BE=4
| 5 |
点评:本题考查了图形的剪拼,仔细观察图形,得到组成正方形的边长的线段是解题的关键.

练习册系列答案
相关题目