题目内容
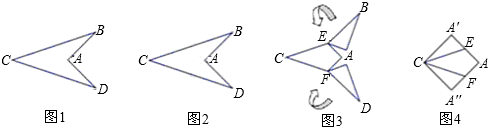
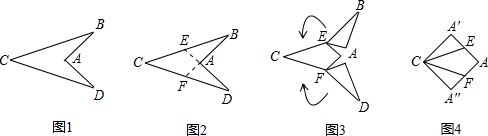
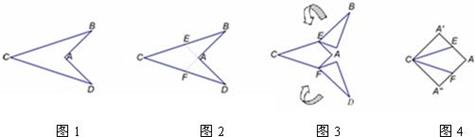
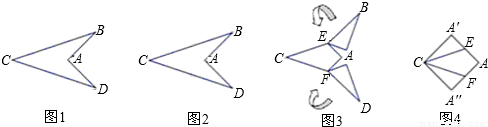
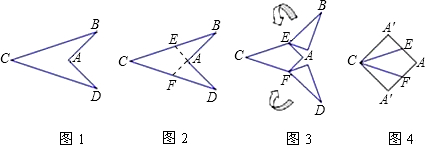
图1中的“箭头”是以AC所在直线为对称轴的轴对称图形，∠BAD=90°，AB=2．图2到图4是将“箭头”沿虚线剪拼成正方形的过程，则图1中BC的长为（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
分析：由正方形的性质可知AB为正方形边长，2AE为正方形边长，又AB=2，在R△ABE中，由勾股定理求BC的长度．
解答：解：由正方形的性质，得AB=AA′=2AE，
又AB=2，∴AE=1，BE=
=
，
再由折叠的性质，得BC=2BE=2
．
故选：D．
又AB=2，∴AE=1，BE=
| AB2+AE2 |
| 5 |
再由折叠的性质，得BC=2BE=2
| 5 |
故选：D．
点评：本题考查轴对称的性质，有一定的难度，关键在于结合图形进行解答．
练习册系列答案
口算能手系列答案
相关题目
