题目内容
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.

(1)求证:BE是⊙O的切线;
![]() (2)若BC=
(2)若BC=![]() ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长.
【答案】(1)详见解析;(2)R=3,BE=![]() .
.
【解析】
试题分析:(1)连接OB,根据已知条件易证∠EBD=∠CAB,继而得到∠BAD=∠EBD,根据直径所对的圆周角为直角即可证得结论;(2)连接CD,交OB于点F,易证OF为三角形ADC的中位线,根据三角形的中位线定理求得OF,再用平行线分线段成比例定理求出半径R,最后用切割线定理即可.
试题解析:(1)如图,
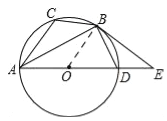
连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线,
(2)如图2,
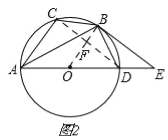
设圆的半径为R,连接CD,
∵AD为⊙O的直径,
∴∠ACCD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF=![]() AC=
AC=![]() ,
,
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴![]() ,
,
即![]() ,
,
∴DE=![]() ,
,
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴![]() ,
,
∴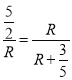 ,
,
∵R>0,
∴R=3,
∵BE是⊙O的切线,
∴BE=![]() .
.

练习册系列答案
相关题目