题目内容
已知双曲线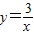 和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.
和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.
【答案】分析:两个函数交点的坐标满足这两个函数关系式,因此,把y=kx+b代入反比例函数解析式,消去y,即可得到一个关于x的一元二次方程,x1与x2就是这个方程的两根.再根据根与系数的关系即可解得k的值.
解答:解:由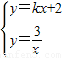 ,
,
得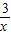 =kx+2,
=kx+2,
kx2+2x-3=0.
∴x1+x2=-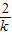 ,x1•x2=-
,x1•x2=-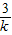 .(2分)
.(2分)
故x12+x22=(x1+x2)2-2x1•x2=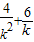 =10.
=10.
∴5k2-3k-2=0,
∴k1=1或k2=- .(4分)
.(4分)
又△=4+12k>0,即k>- ,舍去k2=-
,舍去k2=- ,
,
故所求k值为1.(6分)
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.
解答:解:由
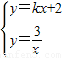 ,
,得
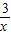 =kx+2,
=kx+2,kx2+2x-3=0.
∴x1+x2=-
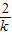 ,x1•x2=-
,x1•x2=-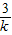 .(2分)
.(2分)故x12+x22=(x1+x2)2-2x1•x2=
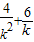 =10.
=10.∴5k2-3k-2=0,
∴k1=1或k2=-
 .(4分)
.(4分)又△=4+12k>0,即k>-
 ,舍去k2=-
,舍去k2=- ,
,故所求k值为1.(6分)
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和直线y=2x-1相交于两点M(a,5)和点N.
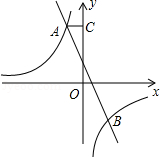
和直线y=2x-1相交于两点M(a,5)和点N. 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=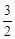 .
.
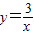 和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.
和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.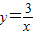 和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.
和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且x12+x22=10,求k的值.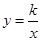 和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.