题目内容
在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;

(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;

(1)∵抛物线y=ax2+bx+2过点A(-3,0),B(1,0),
∴
解得
,
∴二次函数的关系解析式为y=-
x2-
x+2;
(2)存在.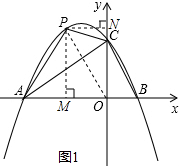
∵如图1所示,设点P坐标为(m,n),则n=-
m2-
m+2.
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
则PM=-
m2-
m+2,PN=-m,AO=3.
∵当x=0时,y=-
×0-
×0+2=2,
∴OC=2,
∴S△PAC=S△PAO+S△PCO-S△ACO
=
AO•PM+
CO•PN-
AO•CO
=
×3×(-
m2-
m+2)+
×2×(-m)-
×3×2
=-m2-3m
∵a=-1<0
∴函数S△PAC=-m2-3m有最大值
∴当m=-
=-
时,S△PAC有最大值.
∴n=-
m2-
m+2=-
×(-
)2-
×(-
)+2=
,
∴存在点P(-
,
),使△PAC的面积最大.
(3)如图2所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q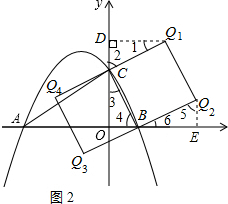 3,则点Q1,Q2,Q3,Q4为符合题意要求的点.过Q1点作Q1D⊥y轴于点D,过点Q2作Q2E⊥x轴于点E,
3,则点Q1,Q2,Q3,Q4为符合题意要求的点.过Q1点作Q1D⊥y轴于点D,过点Q2作Q2E⊥x轴于点E,
∵∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,
∴∠1=∠3,∠2=∠4,
在△Q1CD与△CBO中,
∵
,
∴△Q1CD≌△CBO,
∴Q1D=OC=2,CD=OB=1,
∴OD=OC+CD=3,
∴Q1(2,3);
同理可得Q4(-2,1);
同理可证△CBO≌△BQ2E,
∴BE=OC=2,Q2E=OB=1,
∴OE=OB+BE=1+2=3,
∴Q2(3,1),
同理,Q3(-1,-1),
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(-1,-1),Q4(-2,1).
∴
|
解得
|
∴二次函数的关系解析式为y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)存在.

∵如图1所示,设点P坐标为(m,n),则n=-
| 2 |
| 3 |
| 4 |
| 3 |
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
则PM=-
| 2 |
| 3 |
| 4 |
| 3 |
∵当x=0时,y=-
| 2 |
| 3 |
| 4 |
| 3 |
∴OC=2,
∴S△PAC=S△PAO+S△PCO-S△ACO
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=-m2-3m
∵a=-1<0
∴函数S△PAC=-m2-3m有最大值
∴当m=-
| b |
| 2a |
| 3 |
| 2 |
∴n=-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 2 |
∴存在点P(-
| 3 |
| 2 |
| 5 |
| 2 |
(3)如图2所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q
 3,则点Q1,Q2,Q3,Q4为符合题意要求的点.过Q1点作Q1D⊥y轴于点D,过点Q2作Q2E⊥x轴于点E,
3,则点Q1,Q2,Q3,Q4为符合题意要求的点.过Q1点作Q1D⊥y轴于点D,过点Q2作Q2E⊥x轴于点E,∵∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,
∴∠1=∠3,∠2=∠4,
在△Q1CD与△CBO中,
∵
|
∴△Q1CD≌△CBO,
∴Q1D=OC=2,CD=OB=1,
∴OD=OC+CD=3,
∴Q1(2,3);
同理可得Q4(-2,1);
同理可证△CBO≌△BQ2E,
∴BE=OC=2,Q2E=OB=1,
∴OE=OB+BE=1+2=3,
∴Q2(3,1),
同理,Q3(-1,-1),
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(-1,-1),Q4(-2,1).

练习册系列答案
相关题目
 的长是方程x2-6x+5=0的两个实数根.
的长是方程x2-6x+5=0的两个实数根.


