题目内容

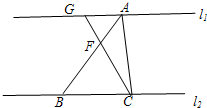（2013•奉贤区一模）如图，已知l1∥l2，点A、G、B、C分别在l1和l2上，AF=
2
5
AB．
（1）求
AG
BC
的值；
（2）若
AB
=
a
，
AC
=
b
，用向量
a
与
b
表示
AG
．
分析：（1）根据平行线的性质可得
AG
BC
=
AF
FB
，结合，AF=
2
5
AB即可得出答案；
（2）先表示出
CB
，结合（1）的结论即可得出
AG
．
解答：解：（1）∵AF=
2
5
AB，
∴
AF
FB
=
2
3
，
又∵l1∥l2，
∴
AG
BC
=
AF
FB
=
2
3
．

（2）∵
AB
=
a
，
AC
=
b
，
∴
CB
=
AB
-
AC
=
a
-
b
，
∴
AG
=
2
3
BC
=
2
3
（
a
-
b
）．
点评：本题考查了平面向量的加减及平行线的性质，属于基础题，根据题意得出线段的比值是解答本题的关键．
练习册系列答案
相关题目
（2013•奉贤区一模）抛物线y=ax2（a＞0）的图象一定经过
一二
一二
象限．
（2013•奉贤区一模）已知三角形三边长为3、4、5，则最小角的正弦是
3
5
3
5
．
（2013•奉贤区一模）若⊙O的一条弦长为24，弦心距为5，则⊙O的直径长为
26
26
．
（2013•奉贤区一模）在Rt△ABC中，∠C=90°，AB=5，BC=3，点D、E分别在BC、AC上，且BD=CE，设点C关于DE的对称点为F，若DF∥AB，则BD的长为
1
1
．
（2013•奉贤区一模）计算：
2cos30°+3cot60°2sin60°-tan245°
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网