Question

【题目】已知：如图，在△ABC中，点E、F分别在边AB、AC上，EF∥BC,且EF=BC．延长EF到点G，使得FG=EF，连接CG．

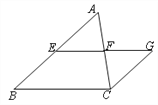
（1）求证：四边形BCGE是平行四边形；

（2）求证：E、F分别是AB、AC的中点．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】（1）∵EF= BC，FG=EF，∴EG=BC．

又∵EF∥BC，∴四边形BCGE是平行四边形．

（2）∵四边形BCGE是平行四边形．∴AB∥GC，BE=GC，∴∠A=∠FCG，

在△AEF和△CGF中，∠A＝∠FCG，∠AFE＝∠CFG，EF＝FG，∴△AEF≌△CGF（AAS）．

∴AF=FC，AE=GC，又∵BE=GC，∴AE=BE，即E、F分别是AB、AC的中点．