题目内容
【题目】观察下面三行数：
第一行：
···
第二行：
···
第三行 ：
···
探索它们之间的关系,寻求规律解答下列问题：
直接写出第②行数的第
个数是_____ ；
直接写出第二行第
个数是 ，第三行第个数是
取每行的第个数,请判断是否存在这样的
个数使它们的和为
,并说明理由．
【答案】（1）259；（2）
，
；（3）这
个数不存在，理由见解析
【解析】
（1）根据题目中数字的特点，第二行的每个数比第一行的多3，第三行的每个数比第一行的相反数多3，可以写出每行第n个式子，从而可以得到第二行第8个数；
（2）根据（1）中发现的数字的特点，可以直接写出第二行第n个数和第三行第n个数；
（3）先判断是否存在，再根据题目中数字的特点可以说明理由，本题得以解决．
（1）∵第一行：-2、4、-8、16、-32、64…
第二行：1、7、-5、19、-29、67…
第三行：5、-1、11、-13、35、-61…
通过观察得到：
第一行：
、
、
、
、
第
个数为：
，
第二行：
、
、
、
、第个数为：，
第三行：
、
、
、
、第个数为：，
∴第二行数的第8个数是：
，
故答案为：259；
（2）由（1）可知，
第二行第个数为：，
第三行第个数为：，
故答案为：，；
（3）取每行的第个数，不存在这样的3个数使它们的和为134，
理由如下：
设第一行的第个数为
，则第二行第个数为
，第三行第n个数为
，
，
解得：
，
令
，因为n是正整数，所以不存在，
即128在第一行不存在，
故取每行的第n个数，不存在这样的3个数使它们的和为134．
【题目】时代中学从学生兴趣出发，实施体育活动课走班制.为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1200名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
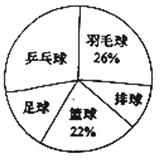
解答下列问题：
（1）这次抽样调查中的样本是________；
（2）统计表中，
________，
________；
（3）试估计上述1200名学生中最喜欢乒乓球运动的人数.
