题目内容
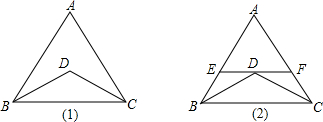 如图(1),AB=AC,BD平分∠ABC,CD平分∠ACB,则:
如图(1),AB=AC,BD平分∠ABC,CD平分∠ACB,则:(1)图中有
2
2
个等腰三角形;(2)若过D作EF∥BC交AB于E,交AC于F,则图(2)中又增加了
3
3
个等腰三角形.分析:(1)由AB=AC,BD平分∠ABC,CD平分∠ACB,根据等腰三角形的判定与性质,易证得:△ABC与△DBC是等腰三角形;
(2)由EF∥BC,易证得△AEF是等腰三角形,又由BD平分∠ABC,CD平分∠ACB,易证得△EBD和△FDC是等腰三角形,继而求得答案.
(2)由EF∥BC,易证得△AEF是等腰三角形,又由BD平分∠ABC,CD平分∠ACB,易证得△EBD和△FDC是等腰三角形,继而求得答案.
解答:解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=
∠ABC,∠DCB=
∠ACB,
∴∠DBC=∠DCB,
∴DB=DC,
∴△ABC与△DBC是等腰三角形;
(2)∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∵∠ABC=∠ACB,
∴∠AEF=∠AFE,
∴AE=AF,即△AEF是等腰三角形,
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵∠ABD=∠DBC,∠ACD=∠DCB,
∴∠EDB=∠ABD,∠FDC=∠ACD,
∴EB=ED,FD=FC,
即△EBD和△FDC是等腰三角形.
∴又增加了3个.
故答案为:(1)2,(2)3.
∴∠ABC=∠ACB,
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DBC=∠DCB,
∴DB=DC,
∴△ABC与△DBC是等腰三角形;
(2)∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∵∠ABC=∠ACB,
∴∠AEF=∠AFE,
∴AE=AF,即△AEF是等腰三角形,
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵∠ABD=∠DBC,∠ACD=∠DCB,
∴∠EDB=∠ABD,∠FDC=∠ACD,
∴EB=ED,FD=FC,
即△EBD和△FDC是等腰三角形.
∴又增加了3个.
故答案为:(1)2,(2)3.
点评:此题考查了等腰三角形的性质与判定以及平行线的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 6、如图所示,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=20°,则∠EOF=
6、如图所示,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=20°,则∠EOF=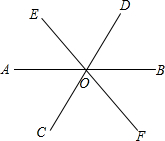 如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF=60°,求∠BOD的度数.
如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF=60°,求∠BOD的度数.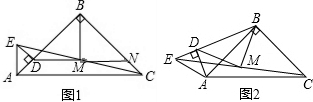
 22、(初三)如图,△ABC中,AB=AC,I为△ABC的内心,AI的延长线交△ABC的外接圆于点D,过点I作BC的平行线分别交AB、AC于E、F,若O是△DEF外接圆的圆心.
22、(初三)如图,△ABC中,AB=AC,I为△ABC的内心,AI的延长线交△ABC的外接圆于点D,过点I作BC的平行线分别交AB、AC于E、F,若O是△DEF外接圆的圆心.
 (1)解不等式组:
(1)解不等式组: