题目内容
【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
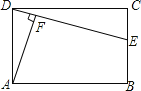
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长.
【答案】(1)见解析;(2)CE=3.
【解析】
试题分析:(1)根据四边形ABCD是矩形可得出∠ADC=∠C=90°,再根据相似三角形的判定定理可得出△ADF∽△DCE,由相似三角形的对应边成比例即可得出结论;
(2)由(1)可知DF:AF=CE:DC,再结合已知条件即可求出CE的长.
(1)证明:
∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,
∴∠ADF+∠CDE=90°,
∵AF⊥DE,
∴∠AFD=∠DAF+∠FDA=90°,
∴∠FAD=∠CDE,
又∵∠C=∠AFD=90°,
∴△ADF∽△DCE;
∴![]() ,
,
即DFCD=AFCE;
(2)∵△ADF∽△DCE;
∴![]() ,
,
∴![]() ,
,
又∵AF=4DF,CD=12,
∴![]() ,
,
∴CE=3.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
