题目内容
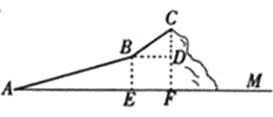
【题目】今年“五一”假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山巅C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,点C到水平线AM的距离为600米.
(1)求B点到水平线AM的距离.
(2)求斜坡AB的坡度.

【答案】(1) 400(米);(2) 1:2.4.
【解析】试题分析:(1)过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,构造直角三角形ABE和直角三角形CBD,然后根据直角三角形的性质求出CD的高度,用点B的海拔高度减去CD的长度就是点B的海拔高度;(2)要求斜坡AB的坡度,首先要做的就是求出AB的长度,那么就需要构建直角三角形,运用勾股定理来求解;以及根据坡度的定义求出坡度.
试题解析:解:(1)如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足.
在C点测得B点的俯角为30°,
∴∠CBD=30°,又BC=400米,
∴CD=400×sin30°=400×![]() =200(米).
=200(米).
∴B点的铅直高度为600﹣200=400(米).
(2)∵BE=400米,
∴AB=1040米,AE=![]() =
=![]() =960米,
=960米,
∴AB的坡度iAB=![]() =
=![]() =
=![]() ,
,
故斜坡AB的坡度为1:2.4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


