题目内容

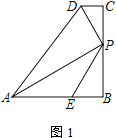
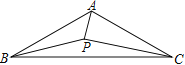
【题目】如图，△ABC中，AB＝AC，点P为△ABC内一点，∠APB＝∠BAC＝120°．若AP＋BP＝4，则PC的最小值为（ ）

A. 2B. C. D. 3

【答案】B

【解析】

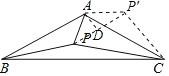
把△APB绕点A逆时针旋转120°得到△AP'C，作AD⊥PP'于D，根据旋转变换的性质和等腰三角形的性质得到∠AP'P=30°，根据直角三角形的性质得到PP'AP，根据勾股定理和配方法计算．

把△APB绕点A逆时针旋转120°得到△AP'C，作AD⊥PP'于D，则AP=AP'，∠PAP'=120°，∠AP'C=∠APB=120°，∴∠AP'P=30°，∴PP'AP，∠PP'C=90°．

∵AP+BP=4，∴BP=4﹣PA．在Rt△PP'C中，PC，则PC的最小值为2．

故选B．

练习册系列答案
相关题目

【题目】如图1，已知点，，且、满足，的边与轴交于点，且为中点，双曲线经过、两点．

（1）求的值；

（2）点在双曲线上，点在轴上，若以点、、、为顶点的四边形是平行四边形，试求满足要求的所有点、的坐标；

（3）以线段为对角线作正方形（如图，点是边上一动点，是的中点，，交于，当在上运动时，的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．

【题目】现有一个六面分别标有数字1，2，3，4，5，6，且质地均匀的正方体筛子，另有三张正面分别标有1，2，3，的卡片（卡片除数字外，其他都相同），先由小明掷筛子一次，记下筛子向上一面出现的数字，然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张，记下卡片上的数字。

（1）请用列表或树状图的方法，求出筛子向上一面出现的数字与卡片上的数字之积为6的概率；

（2）小明和小王做游戏，约定游戏规则如下：若筛子向上一面出现的数字与卡片上的数字之积大于7，则小明赢；若筛子向上一面出现的数字与卡片上的数字之积小于7，则小王赢；问小明和小王谁赢的可能性更大？请说明理由。

【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+x+与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点D是抛物线的顶点．

（1）如图1，P为直线BC上方抛物线上一动点，过点P作PQ∥y轴交BC于点Q．在抛物线的对称轴上有一动点M，在x轴上有一动点N，当6PQ﹣CQ的值最大时，求PM+MN+NB的最小值；

（2）如图2，将△ABC绕点B逆时针旋转90°后得到△A′BC'，再将△A′BC′向右平移1个单位得到△A“B′C“，那么在抛物线的对称轴DM上，是否存在点T，使得△A′B′T为等腰三角形？若存在，求出点T到x轴的距离；若不存在，请说明理由．

【题目】在平面直坐标系中，有A（﹣2，3），B（﹣2，﹣1）两点，若点A关于y轴的对称点为点C，点B向右平移8个单位到点D．

（1）分别写出点C，点D的坐标；

（2）若一次函数图象经过C，D两点，求一次函数表达式．

【题目】四边形ABCD中，AB=BC，∠B=∠C=90°，P是BC边上一点，AP⊥PD，E是AB边上一点，∠BPE=∠BAP．

（1） 如图1，若AE=PE，直接写出=______；

（2） 如图2，求证：AP=PD＋PE；

（3） 如图3，当AE=BP时，连BD，则=______，并说明理由．

【题目】如图，中，是上一点，于点，是的中点，于点，与交于点，若，平分，连接，.

（1）求证：；

（2）小亮同学经过探究发现：.请你帮助小亮同学证明这一结论.

（3）若，判定四边形是否为菱形，并说明理由.

【题目】如图，在△ABC中，∠ACB=90°，AC=4，BC=3，点E、F分别在AC，AB上，连接EF.

（1）将△ABC沿EF折叠，使点A落在AB边上的点D处，如图1，若S四边形ECBD=2S△EDF，求AE的长；

（2）将△ABC沿EF折叠，使点A落在BC边上的点M处，如图2，若MF⊥CB.

①求AE的长；②求四边形AEMF的面积；

（3）若点E在射线AC上，点F在边AB上，点A关于EF所在直线的对称点为点P，问：是否存在以PF、CB为对边的平行四边形，若存在，求出AE的长；若不存在，请说明理由.

【题目】如图，在ABCD中，点P是AB边上一点不与A，B重合，，过点作，交AD边于点Q，连结CQ．

若，求证：四边形ABCD是矩形；

在的条件下，当，时，求AQ的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网