题目内容
 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC.
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC.
(1)求缆绳AC的长.(精确到0.1米)
(2)若在缆绳上有一辆缆车正以1000米每小时的速度从A出发求经过多少分钟后能够到达C(精确到0.1小时)(参考数据: ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24,
≈2.24, ≈2.45)
≈2.45)
 解:作AB⊥CD交CD的延长线于点B,
解:作AB⊥CD交CD的延长线于点B,在Rt△ABC中,∵∠ACB=∠CAE=30°,
∴AC=2AB,
在Rt△ABD中,∵∠ADB=∠EAD=45°,
∴DB=AB,
设AB=x,则BD=x,AC=2x,CB=50+x,
∵tan∠ACB=tan30°=
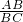 ,
,∴AB=BC•tan∠ACB=BC•tan30°,即x=(50+x)•
 ,
,解得:x=25(1+
 ),
),∴AC=50(1+
 )≈136.5(米),
)≈136.5(米),即缆绳AC的长为136.5米;
(2)t=
 =
= =0.1365(h)≈8.2(分钟),
=0.1365(h)≈8.2(分钟),答:经过8.2分钟后能够到达C.
分析:(1)根据题意构造直角三角形,本题涉及到两个直角三角形△ABC和△ABD,应利用其公共边构造等量关系,进而可求出AC的长度;
(2)根据(1)求得的AC的长度和缆车的速度,容易求得所用的时间.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
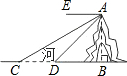 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45度.C、D、B在同一水平线上,又知河宽CD为50米,则山高AB是( )
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45度.C、D、B在同一水平线上,又知河宽CD为50米,则山高AB是( )| A、50米 | ||
| B、25米 | ||
C、25(
| ||
| D、75米 |
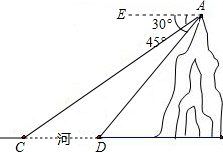 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号).
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号).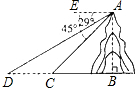 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为45°,测得岸边点D的俯角为29°,又知河宽CD为60米.现需从河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长.(精确到0.1).
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为45°,测得岸边点D的俯角为29°,又知河宽CD为60米.现需从河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长.(精确到0.1).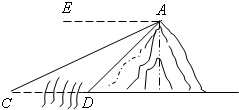 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC=120米,求河宽CD的长?
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC=120米,求河宽CD的长?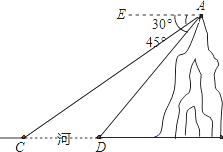 (2012•沙河口区模拟)如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC.
(2012•沙河口区模拟)如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC.