题目内容
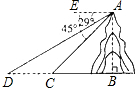 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为45°,测得岸边点D的俯角为29°,又知河宽CD为60米.现需从河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长.(精确到0.1).
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为45°,测得岸边点D的俯角为29°,又知河宽CD为60米.现需从河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长.(精确到0.1).参考数据:sin29°≈0.48,cos29°≈0.87,tan 29°≈0.55,tan61°≈l.80,
| 2 |
分析:先利用直角三角形的性质求出∠DAB的度数,由锐角三角函数的定义可知DB=AB•tan61°,在Rt△ABC中,由∠ACB=∠CAB=45°,可知BC=AB,再根据DC=DB-BC可求出AB的长,利用锐角三角函数的定义即可得出AC的长.
解答:解:在RT△ABD中,∠DAB=90°-29°=61°
∴DB=AB•tan61°,
在Rt△ABC中,∠ACB=∠CAB=45°,BC=AB,
∵DC=DB-BC,
∴60=AB•tan61°-AB,
∴AB=
≈
=75,
∴AC=
=
=75
≈75×1.41=105.75≈105.8(米),
故缆绳AC的长约为105.8米.
∴DB=AB•tan61°,
在Rt△ABC中,∠ACB=∠CAB=45°,BC=AB,
∵DC=DB-BC,
∴60=AB•tan61°-AB,
∴AB=
| 60 |
| tan61°-1 |
| 60 |
| 1.80-1 |
∴AC=
| AB |
| sin45° |
| 75 | ||||
|
| 2 |
故缆绳AC的长约为105.8米.
点评:本题考查的是解直角的应用-仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
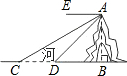 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45度.C、D、B在同一水平线上,又知河宽CD为50米,则山高AB是( )
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45度.C、D、B在同一水平线上,又知河宽CD为50米,则山高AB是( )| A、50米 | ||
| B、25米 | ||
C、25(
| ||
| D、75米 |
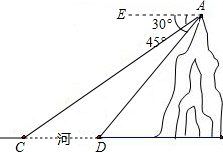 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号).
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号).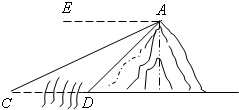 如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC=120米,求河宽CD的长?
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC=120米,求河宽CD的长?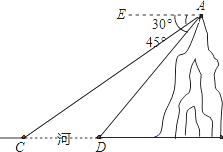 (2012•沙河口区模拟)如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC.
(2012•沙河口区模拟)如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC.