题目内容
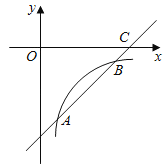
【题目】如图,已知,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,点
,点![]() 是该抛物线上不与
是该抛物线上不与![]() 重合的动点,过点
重合的动点,过点![]() 作
作![]() 轴于
轴于![]() ,交直线
,交直线![]() 于点
于点![]() .
.
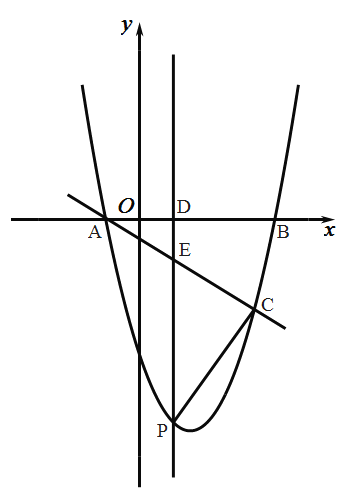
(1)求抛物线的解析式;
(2)若![]() ,当
,当![]() 时,求点
时,求点![]() 坐标;
坐标;
(3)当(2)中直线![]() 为
为![]() 时,是否存在实数
时,是否存在实数![]() ,使
,使![]() 与
与![]() 相似?若存在请求出
相似?若存在请求出![]() 的值;若不存在,请说明你的理由.
的值;若不存在,请说明你的理由.
【答案】(1)![]() ;(2)(5,6)或(1,-6);(3)存在,-2或-1
;(2)(5,6)或(1,-6);(3)存在,-2或-1
【解析】
(1)把A.B两点的坐标代入![]() ,利用待定系数法可求得抛物线解析式;
,利用待定系数法可求得抛物线解析式;
(2)设出P点坐标,则可表示出E.D的坐标,从而可表示出PE和DE的长,由条件可得关于P点坐标的方程,则可求得P点坐标;
(3)分两种情况![]() 或
或![]() ,
,![]() 时,由二次函数的对称性得出C点坐标,代入
时,由二次函数的对称性得出C点坐标,代入![]() 即可求解;
即可求解;![]() 时,如图2,过
时,如图2,过![]() 点作
点作![]() 于点
于点![]() ,由相似三角形的性质及二次函数的对称性得出C点、F点坐标,进而可求得k的值.
,由相似三角形的性质及二次函数的对称性得出C点、F点坐标,进而可求得k的值.
解:(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为![]() ;
;
(2)当![]() 时,直线
时,直线![]() 的解析式为
的解析式为![]() .
.
设![]() ,
,
则![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
当![]() 时,
时,
解得![]() 或
或![]() ,
,
但当![]() 时,
时,![]() 与
与![]() 重合不合题意,舍去,
重合不合题意,舍去,
∴![]() ;
;
当![]() 时,
时,
解得![]() 或
或![]() ,
,
但当![]() 时,
时,![]() 与
与![]() 重合不合题意,舍去,
重合不合题意,舍去,
∴![]() ;
;
综上可知![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
(3)存在.
∵![]() ,
,
∴要使![]() 与
与![]() 相似,
相似,
必有![]() 或
或![]() ,
,
①当![]() 时,
时,
如图1,![]() 轴,
轴,
图1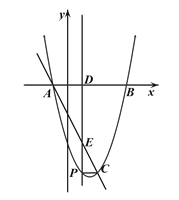
∵![]() ,根据对称性可得
,根据对称性可得![]() ,
,
将![]() 代入
代入![]() 解析式中,
解析式中,
得![]() ,
,
解得,![]() ,
,
②当![]() 时,
时,
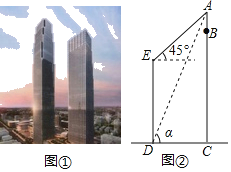
如图2,过![]() 点作
点作![]() 于点
于点![]() ,
,
图2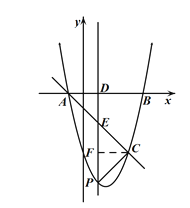
则有![]() ,
,
则![]() ,
,
∴![]() ,
,
易得![]() ,
,
∴![]() ,
,
由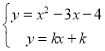
得![]() 或
或![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴ ![]() ,
,
解得,![]() ,
,![]() (此时
(此时![]() 与
与![]() 重合,舍去)
重合,舍去)
综上,当![]() 或
或![]() 时,
时,![]() 与
与![]() 相似.
相似.

【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为A、B、C、D四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩 | 等级 | 人数 |
| A | 12 |
| B | m |
| C | n |
| D | 9 |
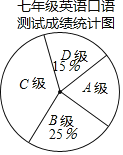
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中C级的圆心角度数;
(3)若该校七年级共有学生640人,根据抽样结课,估计英语口语达到B级以上![]() 包括B级
包括B级![]() 的学生人数.
的学生人数.