题目内容
【题目】我们提供如下定理:在直角三角形中,30°的锐角所对的直角边是斜边的一半,
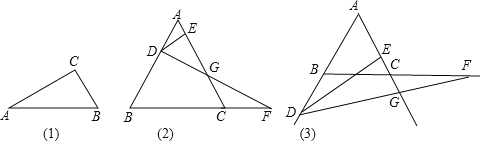
如图(1),Rt△ABC中,∠C=90°,∠A=30°,则BC=![]() AB.
AB.
请利用以上定理及有关知识,解决下列问题:
如图(2),边长为6的等边三角形ABC中,点D从A出发,沿射线AB方向有A向B运动点F同时从C出发,以相同的速度沿着射线BC方向运动,过点D作DE⊥AC,DF交射线AC于点G.
(1)当点D运动到AB的中点时,直接写出AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
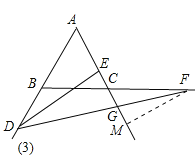
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图3的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,说明理由.
【答案】(1)AE =![]() ;(2)AD=2,S△BDF=8
;(2)AD=2,S△BDF=8![]() ;(3)不变,理由见解析
;(3)不变,理由见解析
【解析】
(1)根据D为AB的中点,求出AD的长,在Rt△ADE中,利用30°所对的直角边等于斜边的一半求出AE的长即可;
(2)根据题意得到设AD=CF=x,表示出BD与BF,在Rt△BDF中,利用30°所对的直角边等于斜边的一半得到BF=2BD,列出关于x的方程,求出方程的解得到x的值,确定出BD与BF的长,利用勾股定理求出DF的长,即可确定出△BDF的面积;
(3)不变,理由如下,如图,过F作FM⊥AG延长线于M,由AD=CF,且△ABC为等边三角形,利用等边三角形的性质及锐角三角函数定义得到DE=FM,以及AE=CM,利用AAS得到△DEG与△FMC全等,利用全等三角形对应边相等得到EG=MG,根据AC=AE+EC,等量代换即可得证.
解:(1)当D为AB中点时,AD=BD=![]() AB=3,
AB=3,
在Rt△ADE中,∠A=60°,
∴∠ADE=30°,
∴AE=![]() AD=
AD=![]() ;
;
(2)设AD=x,∴CF=x,
则BD=6-x,BF=6+x,
∵∠B=60°,∠BDF=90°,
∴∠F=30°,即BF=2BD,
∴6+x=2×(6-x),
解得:x=2,即AD=2,
∴BD=4,BF=8,
根据勾股定理得:DF=![]() 4
4![]() ,
,
∴S△BDF=![]() ×4×4
×4×4![]() =8
=8![]() ;
;
(3)不变,理由如下,如图,过F作FM⊥AG延长线于M,
∵△ABC为等边三角形,
∴∠A=∠ACB=∠FCM=60°,
在Rt△ADE和Rt△FCM中,
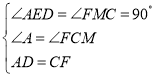
∴Rt△ADE≌Rt△FCM,
∴DE=FM,AE=CM,
在△DEG和△FMG,
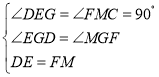 ,
,
∴△DEG≌△FMG,
∴GE=GM,
∴AC=AE+EC=CM+CE=GE+GM=2GE.