题目内容
第16届亚运会将于2010年11月12日在广州开幕,其吉祥物为运动时尚的五只羊,分别取名“阿祥”、“阿和”、“阿如”、“阿意”、“乐羊羊”,某工艺厂工人小李负责生产“阿祥”、“乐羊羊”的生产,以下是某月工作的部分信息:信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产“阿祥”、“乐羊羊”两个产品,并且按规定每月生产“阿祥”的
 个数不少于90个.生产吉祥物个数与所用时间之间的关系见下表:
个数不少于90个.生产吉祥物个数与所用时间之间的关系见下表:| 生产“阿祥”个数 | 生产“乐羊羊”个数 | 所用总时间(分) |
| 1 | 2 | 40 |
| 3 | 4 | 90 |
根据以上信息,回答下列问题:
(1)小李每生产一个“阿祥”,每生产一个“乐羊羊”分别需要多少分钟?
(2)小李该月最多能得多少元工资?此时生产“阿祥”、“乐羊羊”分别多少个?
分析:(1)设生产一个“阿祥”需x分,生产一个“乐羊羊”需y分;按照等量关系“一个月工作总时间=生产“阿祥”的时间+生产“乐羊羊”的时间”,列出二元一次方程求解.
(2)设出生产“阿祥”和“乐羊羊”的数量分别为x,y;根据等量关系“一个月工作总时间=生产“阿祥”的时间+生产“乐羊羊”的时间”列出等式,再将工资总额用设出的其中一个量表示出来,根据条件,生产“阿祥”不少于90个,求出最大值.
(2)设出生产“阿祥”和“乐羊羊”的数量分别为x,y;根据等量关系“一个月工作总时间=生产“阿祥”的时间+生产“乐羊羊”的时间”列出等式,再将工资总额用设出的其中一个量表示出来,根据条件,生产“阿祥”不少于90个,求出最大值.
解答:解:(1)设生产一个“阿祥”需x分,生产一个“乐羊羊”需y分,由题意得:
(3分)
解这个方程组得:
(2分)
(2)设生产“阿祥”x个,生产“乐羊羊”y个,则生产“阿祥”共用10x分,生产“乐羊羊”共用15y分.
又一个月工作25×8×60分,则10x+15y=25×8×60
∴w总额=1.8x+3×
=-0.2x+2400
又x≥90,
当x=90时,w取得最大值,此时w=2382(元)
“阿祥”有90(个),“乐羊羊”有740(个),能得2382元.
|
解这个方程组得:
|
(2)设生产“阿祥”x个,生产“乐羊羊”y个,则生产“阿祥”共用10x分,生产“乐羊羊”共用15y分.
又一个月工作25×8×60分,则10x+15y=25×8×60
∴w总额=1.8x+3×
| 25×8×60-10x |
| 15 |
又x≥90,
当x=90时,w取得最大值,此时w=2382(元)
“阿祥”有90(个),“乐羊羊”有740(个),能得2382元.
点评:此题为综合应用题,考查学生对题中信息的理解能力,同时需借助方程、函数性质求得结果.

练习册系列答案
相关题目
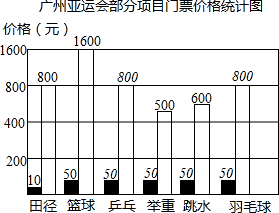 (2010•资阳)第16届亚运会将于2010年11月12日至27日在中国广州进行,各类门票现已开始销售.若部分项目门票的最低价和最高价如图所示,则这六个项目门票最高价的中位数是
(2010•资阳)第16届亚运会将于2010年11月12日至27日在中国广州进行,各类门票现已开始销售.若部分项目门票的最低价和最高价如图所示,则这六个项目门票最高价的中位数是