题目内容
附加题:用换元法解方程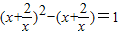 ,若设y=x+
,若设y=x+ ,则原方程可化为( )
,则原方程可化为( )A.y2-y+1=0
B.y2+y+1=0
C.y2+y-1=0
D.y2-y-1=0
【答案】分析:设y=x+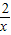 ,即可把原方程化为整式方程.
,即可把原方程化为整式方程.
解答:解:设y=x+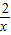 ,
,
∴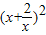 =y2,
=y2,
∴原方程可化为y2-y=1,
进一步化简得:y2-y-1=0.
故选D.
点评:当分式方程比较复杂时,通常采用换元法使分式方程简化.
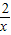 ,即可把原方程化为整式方程.
,即可把原方程化为整式方程.解答:解:设y=x+
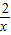 ,
,∴
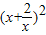 =y2,
=y2,∴原方程可化为y2-y=1,
进一步化简得:y2-y-1=0.
故选D.
点评:当分式方程比较复杂时,通常采用换元法使分式方程简化.

练习册系列答案
相关题目
附加题:用换元法解方程(x+
)2-(x+
)=1,若设y=x+
,则原方程可化为( )
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| A、y2-y+1=0 |
| B、y2+y+1=0 |
| C、y2+y-1=0 |
| D、y2-y-1=0 |
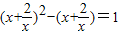 ,若设y=x+
,若设y=x+ ,则原方程可化为( )
,则原方程可化为( )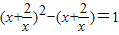 ,若设y=x+
,若设y=x+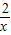 ,则原方程可化为( )
,则原方程可化为( )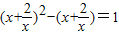 ,若设y=x+
,若设y=x+ ,则原方程可化为( )
,则原方程可化为( )