题目内容
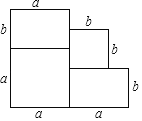
【题目】如图是一所住宅的建筑平面图．
（1）用含有a、b的式子表示这所住宅的建筑面积．
（2）当a＝5米，b＝4米时，住宅的建筑面积有多大？
（3）在（2）的条件下，若此住宅的销售单价为每平方米5000元，求此住宅的销售价是多少元？（结果用科学记数法表示）
【答案】（1）a2+2ab+b2．（2）当a＝5米，b＝4米时，住宅的建筑面积为81平方米．（3）4.05×105元．
【解析】
（1）根据正方形和长方形面积公式即可求解；
（2）将已知数据代入（1）中求得的代数式，即可求解；
（3）根据销售单价乘以建筑面积即可求得销售价．
解：（1）根据图形，得
住宅面积为：a2+2ab+b2．
答：这所住宅的建筑面积为a2+2ab+b2．
（2）把a＝5，b＝4代入a2+2ab+b2得
52+2×5×4+42＝81
答：当a＝5米，b＝4米时，住宅的建筑面积为81平方米．
（3）根据题意，得
81×5000＝405000＝4.05×105．
答：此住宅的销售价是4.05×105元．
新思维寒假作业系列答案【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售，其进价与标价如下表：
LED 灯泡 | 普通白炽灯泡 | |
进价（元） | 45 | 25 |
标价（元） | 60 | 30 |
（1）该商场购进了 LED 灯泡与普通白炽灯泡共 300 个，LED 灯泡按标价进行销售，而普通 白炽灯泡打九折销售，当销售完这批灯泡后可获利 3 200 元，求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个？
（2）由于春节期间热销，很快将两种灯泡销售完，若该商场计划再次购进这两种灯泡 120 个， 在不打折的情况下，请问如何进货，销售完这批灯泡时获利最多且不超过进货价的 30%， 并求出此时这批灯泡的总利润为多少元？
【题目】（本小题满分18分）某校八（1）班同学为了解2011年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，
月均用水量 | 频数（户） | 频率 |
| 6 | 0．12 |
| 0．24 | |
| 16 | 0．32 |
| 10 | 0．20 |
| 4 | |
| 2 | 0．04 |
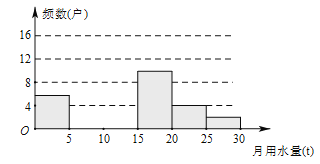
请解答以下问题：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）若该小区用水量不超过15t的家庭占被调查家庭总数的百分比；
（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20 t的家庭大约有多少户？
