题目内容
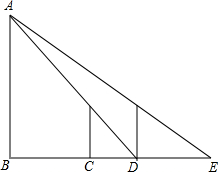如图，一天晚上，小颖由路灯A下的B处走到C处时，测得影子CD的长为1米，当她继续往前走到D处时，测得此时影子DE的长刚好是自己的身高，已知小颖的身高为1.5米，那么路灯A的高度AB为（ ）| A、3米 | B、4.5米 | C、6米 | D、8米 |
分析：根据已知得出∠E=∠EAB=45°，得出AB=BE，再进而利用△DCE∽△DBA，得出
=
，进而求出即可．
| DC |
| MC |
| BD |
| AB |
解答：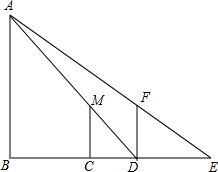
解：∵当她继续往前走到D处时，测得此时影子DE的长刚好是自己的身高，
∴DF=DE=1.5m，
∴∠E=∠EAB=45°，
∴AB=BE，
∵MC∥AB，
∴△DCE∽△DBA，
∴
=
，
设AB=x，则BD=x-1.5=x-1.5，
∴
=
，
解得：x=4.5．
∴路灯A的高度AB为4.5m．
故选：B．
解：∵当她继续往前走到D处时，测得此时影子DE的长刚好是自己的身高，∴DF=DE=1.5m，
∴∠E=∠EAB=45°，
∴AB=BE，
∵MC∥AB，
∴△DCE∽△DBA，
∴
| DC |
| MC |
| BD |
| AB |
设AB=x，则BD=x-1.5=x-1.5，
∴
| 1 |
| 1.5 |
| x-1.5 |
| x |
解得：x=4.5．
∴路灯A的高度AB为4.5m．
故选：B．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出AB=BE是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
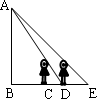
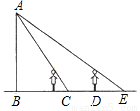
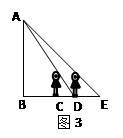
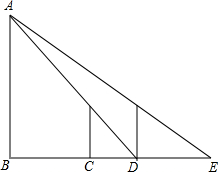如图，一天晚上，小颖由路灯A下的B处走到C处时，测得影子CD的长为1米，当她继续往前走到D处时，测得此时影子DE的长刚好是自己的身高，已知小颖的身高为1.5米，那么路灯A的高度AB为