题目内容
 (2012•兰州)如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是
(2012•兰州)如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是-
≤x≤
且x≠0
| 2 |
| 2 |
-
≤x≤
且x≠0
.| 2 |
| 2 |
分析:由题意得x有两个极值点,过点P与⊙O相切时,x取得极值,作出切线,利用切线的性质求解即可.
解答: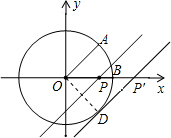 解:将OA平移至P'D的位置,使P'D与圆相切,
解:将OA平移至P'D的位置,使P'D与圆相切,
连接OD,由题意得,OD=1,∠DOP'=45°,∠ODP'=90°,
故可得OP'=
,即x的极大值为
,
同理当点P在y轴左边时也有一个极值点,此时x取得极小值,x=-
,
综上可得x的范围为:-
≤x≤
.
又∵DP'与OA平行,
∴x≠0,
故答案为:-
≤x≤
且x≠0.
 解:将OA平移至P'D的位置,使P'D与圆相切,
解:将OA平移至P'D的位置,使P'D与圆相切,连接OD,由题意得,OD=1,∠DOP'=45°,∠ODP'=90°,
故可得OP'=
| 2 |
| 2 |
同理当点P在y轴左边时也有一个极值点,此时x取得极小值,x=-
| 2 |
综上可得x的范围为:-
| 2 |
| 2 |
又∵DP'与OA平行,
∴x≠0,
故答案为:-
| 2 |
| 2 |
点评:此题主要考查了直线与圆的位置关系,分别得出两圆与圆相切时求出OP的长是解决问题的关键,难度一般,注意两个极值点的寻找.

练习册系列答案
相关题目
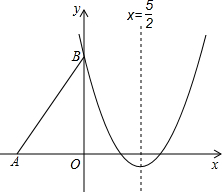 (2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
(2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=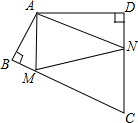 (2012•兰州)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
(2012•兰州)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( ) (2012•兰州)如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是
(2012•兰州)如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y=