题目内容
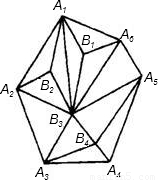
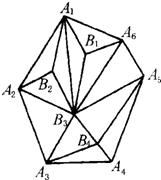13、设多边形A1A2A3…An中，有m个点B1，B2，B3，…，Bm，连接它们成一张互相毗邻的三角形网（n=6，m=4时的情形如图），称每个小三角形为一个“网眼“，求网中共有
（n+2m-2）
个“网眼”（用含n，m的代数式表示）．分析：应先得到“网眼”中所有三角形的内角和，根据三角形的内角和为180°可得三角形的个数．
解答：解：∵每个“网眼”都是三角形，
∴它们的内角总和为S（n，m）×180°，
∵每个内点Bi处的内角和恰为一个圆周角360°，
∴m个内点Bi处的所有内角和为m×360°，
又n边形的内角和为（n-2）×180°，
∴（n-2）×180°+m×360°=S（n，m）×180°，
解得S（n，m）=n+2m-2．
故答案为：n+2m-2．
∴它们的内角总和为S（n，m）×180°，
∵每个内点Bi处的内角和恰为一个圆周角360°，
∴m个内点Bi处的所有内角和为m×360°，
又n边形的内角和为（n-2）×180°，
∴（n-2）×180°+m×360°=S（n，m）×180°，
解得S（n，m）=n+2m-2．
故答案为：n+2m-2．
点评：本题考查图形的变化规律；根据三角形内角总和得到三角形的个数是解决本题的关键．
练习册系列答案
相关题目
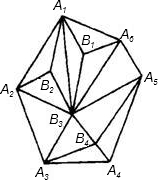设多边形A1A2A3…An中，有m个点B1，B2，B3，…，Bm，连接它们成一张互相毗邻的三角形网（n=6，m=4时的情形如图），称每个小三角形为一个“网眼“，求网中共有________个“网眼”（用含n，m的代数式表示）．
…An是一个有n个顶点的凸多边形，对每一个顶点Ai (i＝1, 2, 3, ……, n)，