ΧβΡΩΡΎ»ί
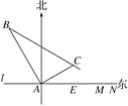
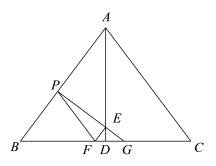
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§AB=AC=5Θ§BC=6Θ§ADΓΆBCΘ§¥ΙΉψΈΣDΘ§ΒψP «±ΏAB…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψPΉςPFΓΈACΫΜœΏΕΈBD”ΎΒψFΘ§ΉςPGΓΆABΫΜAD”ΎΒψEΘ§ΫΜœΏΕΈCD”ΎΒψGΘ§…ηBP=x.
Θ®1Θ©”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈDGΒΡ≥ΛΘΜ
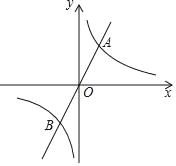
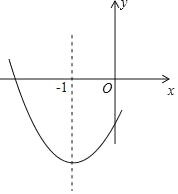
Θ®2Θ©…ηΓςDEFΒΡΟφΜΐΈΣ yΘ§«σy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΕ®“ε”ρΘΜ
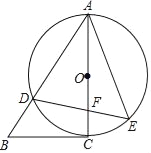
Θ®3Θ©ΓςPEFΡήΖώΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»γΙϊΡήΘ§«σ≥ωBPΒΡ≥ΛΘΜ»γΙϊ≤ΜΡήΘ§«κΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ®
Θ®![]() Θ©ΘΜΘ®3Θ©ΡήΘ§
Θ©ΘΜΘ®3Θ©ΡήΘ§![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟBD=3Θ§Ά®Ιΐ÷ΛΟςΓςABDΓΉΓςGBPΘ§Ω…ΒΟBG=![]() BP=
BP=![]() xΘ§Φ¥Ω…ΒΟDGΒΡ≥ΛΕ»ΘΜ
xΘ§Φ¥Ω…ΒΟDGΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟFD=BD-BF=3-![]() xΘ§DE=
xȧDE=![]() x-
x-![]() Θ§ΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ ΫΩ…«σy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ§ΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ ΫΩ…«σy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©Ζ÷EFΓΆPGΘ§EFΓΆPFΝΫ÷÷«ιΩωΧ÷¬έΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…«σBPΒΡ≥ΛΘ°
Ȯ1ȩÿAB=AC=5ȧBC=6ȧADâBCȧ
ΓύBD=CD=3Θ§
‘ΎRtΓςABD÷–Θ§AD=![]() =4Θ§
=4Θ§
ΓΏΓœB=ΓœBΘ§ΓœADB=ΓœBPG=90ΓψΘ§
ΓύΓςABDΓΉΓςGBPΘ§
Γύ![]() Θ§
Θ§
ΓύBG=![]() BP=
BP=![]() xȧ
xȧ
ΓύDG=BG-BD=![]() x-3ΘΜ
x-3ΘΜ
Ȯ2ȩÿPFøACȧ
ΓύΓςBFPΓΉΓςBCAΘ§
Γύ![]() Θ§
Θ§
Φ¥![]() Θ§
Θ§
ΓύBF=![]() xΘ§
xȧ
ΓύFD=BD-BF=3-![]() xΘ§
xȧ
ΓΏΓœDGE+ΓœDEG=ΓœDGE+ΓœABDΘ§
ΓύΓœABD=ΓœDEGΘ§ΓœADG=ΓœADB=90ΓψΘ§
ΓύΓςDEGΓΉΓςDBAΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύDE=![]() x-
x-![]() Θ§
Θ§
ΓύSΓςDEF=y=![]() ΓΝDFΓΝDE=
ΓΝDFΓΝDE=![]() ΓΝΘ®3-
ΓΝΘ®3-![]() xΘ©ΓΝΘ®
xΘ©ΓΝΘ®![]() x-
x-![]() Θ©=-
Θ©=-![]() x2+
x2+![]() x-
x-![]() Θ®
Θ®![]() ΘΦxΘΦ
ΘΦxΘΦ![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ©»τEFΓΆPG ±Θ§
ÿEFâPGȧEDâFGȧ
ΓύΓœFED+ΓœDEG=90ΓψΘ§ΓœFED+ΓœEFD=90ΓψΘ§
ΓύΓœEFD=ΓœDEGΘ§«“ΓœEDF=ΓœEDGΘ§
ΓύΓςEFDΓΉΓςGDEΘ§
Γύ![]() Θ§
Θ§
ΓύED2=FDΓΝDGΘ§
ΓύΘ®![]() x-
x-![]() Θ©2=Θ®3-
Θ©2=Θ®3-![]() xΘ©Θ®
xΘ©Θ®![]() x-3Θ©Θ§
x-3Θ©Θ§
Γύ5ΓΝ57x2-1138x+225ΓΝ5=0Θ§
Γύx=![]() Θ®≤ΜΚœΧβ“β…α»ΞΘ©Θ§x=
Θ®≤ΜΚœΧβ“β…α»ΞΘ©Θ§x=![]() ΘΜ
ΘΜ
»τEFΓΆPFΘ§
ΓύΓœPFB+ΓœEFD=90ΓψΘ§«“ΓœPFB=ΓœACBΘ§ΓœACB+ΓœDAC=90ΓψΘ§
ΓύΓœEFD=ΓœDACΘ§«“ΓœEDF=ΓœADC=90ΓψΘ§
ΓύΓςEDFΓΉΓςCDAΘ§
Γύ![]() Θ§
Θ§
Γύ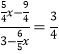 Θ§
Θ§
Γύx=![]() Θ§
Θ§
Ήέ…œΥυ ωΘΚΒ±BPΈΣ![]() Μρ
Μρ![]() ±Θ§ΓςPEFΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°
±Θ§ΓςPEFΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°