题目内容
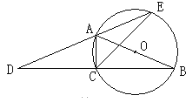
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB= ![]() ,BC-AC=2,求CE的长。
,BC-AC=2,求CE的长。
【答案】(1)、证明过程见解析;(2)、4.
【解析】
试题分析:(1)、根据直径可得∠ACB=90°,根据DC=CB得出AD=AB,从而得出答案;(2)、设BC=x,则AC=x-2,根据△ABC的勾股定理求出x的值,从而得出CE的长度.
试题解析:(1)、∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,
又∵DC=CB,∴AD=AB,∴∠B=∠D;
(2)、设BC=x,则AC=x-2,
在Rt△ABC中,AC2+BC2=AB2,∴(x-2)2+x2=(![]() )2,
)2,
解得x=4或-2(舍去)即BC=4
又∵⊙O中,∠E=∠B,∴∠D=∠E ∴CE=CD=BC=4

练习册系列答案
相关题目