��Ŀ����
��ͼ����֪��һ�κ�����y=-x+4��ͼ���뷴����������y=| 2 | x |
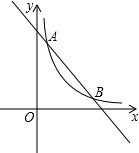 ������ͼ��������һ�㣬��N�ֱ���x�ᡢy�������ߣ�����ֱ�ΪN1��N2�������NN1ON2�����ΪS2��
������ͼ��������һ�㣬��N�ֱ���x�ᡢy�������ߣ�����ֱ�ΪN1��N2�������NN1ON2�����ΪS2����1�������M������Ϊ��x��y������д��S1����x�ĺ�������ʽ������xȡ��ֵʱ��S1�����ֵ��
��2���۲�ͼ�Σ�ͨ��ȷ��x��ȡֵ���ԱȽ�S1��S2�Ĵ�С��
��������1����֪M�����꣬����M����һ�κ�����y=-x+4��ͼ���ϣ������M����������x��ʾ�������Ӷ���ʾ������MM1OM2�����ΪS1����2���۲�ͼ��S1��S2���۲췴����������һ�κ����Ϸ������·����Ӷ��Ƚ����С��
���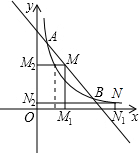 �⣺��1����M������Ϊ��x��y����M���ں���y=-x+4��ͼ���ϣ�
�⣺��1����M������Ϊ��x��y����M���ں���y=-x+4��ͼ���ϣ�
��y=-x+4��
��S1=xy=x��-x+4��=-x2+4x=-��x-2��2+4��
��x=2ʱ��S1���ֵ=4��
��2����N��x1��y1������N�ڷ���������y=
ͼ���ϣ�
��S2=x1��y1=2��
��S1=S2�ɵã�-x2+4x=2����x2-4x+2=0��
��x=2��
��
ͨ���۲�ͼ��ɵã�
��x=2��
ʱ��S1=S2��
��0��x��2-
��2+
��x��4ʱ��S1��S2��
��2-
��x��2+
ʱ��S1��S2��
 �⣺��1����M������Ϊ��x��y����M���ں���y=-x+4��ͼ���ϣ�
�⣺��1����M������Ϊ��x��y����M���ں���y=-x+4��ͼ���ϣ���y=-x+4��
��S1=xy=x��-x+4��=-x2+4x=-��x-2��2+4��
��x=2ʱ��S1���ֵ=4��
��2����N��x1��y1������N�ڷ���������y=
| 2 |
| x |
��S2=x1��y1=2��
��S1=S2�ɵã�-x2+4x=2����x2-4x+2=0��
��x=2��
| 2 |
ͨ���۲�ͼ��ɵã�
��x=2��
| 2 |
��0��x��2-
| 2 |
| 2 |
��2-
| 2 |
| 2 |
���������⿼��һ�κ����ͷ��������������ʼ�Ӧ�ã�ѧ��ͨ��ͼ��Ƚ�����Ĵ�С���Ƚϼ�

��ϰ��ϵ�д�
 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
�����Ŀ
 x��ֵ��
x��ֵ��
 ��ͼ��ͷ���������
��ͼ��ͷ��������� ��ͼ����������㣮
��ͼ����������㣮  �������
�������  =0�Ľ⣨��ֱ��д���𰸣���
=0�Ľ⣨��ֱ��д���𰸣��� <0�Ľ⼯����ֱ��д���𰸣�
<0�Ľ⼯����ֱ��д���𰸣�
 ��һ�κ���
��һ�κ��� ��ͼ��ͷ���������
��ͼ��ͷ��������� ��ͼ����������㣬ֱ��AB��x��Ľ���ΪC��
��ͼ����������㣬ֱ��AB��x��Ľ���ΪC�� �������
�������