��Ŀ����
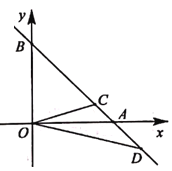
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��AB�ֱ�y�ᡢx���ڵ�A��0��a������B��b��0������a��b����a2-4a+4+![]() ��0��
��0��
��1����a��b��ֵ��
��2����ABΪ����Rt��ABC����C��ֱ��AB���Ҳ࣬�ҡ�ACB��45�������C�����ꣻ
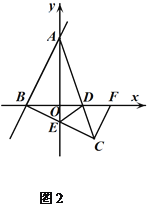
��3������2���ĵ�C�ڵ������ޣ���ͼ2����AC�� x�ύ�ڵ�D��BC��y�ύ�ڵ�E������ DE������C��CF��BC��x���ڵ�F��
����֤��CF=![]() BC��
BC��
��ֱ��д����C��DE�ľ��룮
���𰸡���1��a��2��b��-1����2�����������ĵ�C��2��1����1��-1������3����֤������������1��
��������
��1���ɵ�(a2)2+![]() ��0���ɷǸ��������ʿɵó��𰸣�
��0���ɷǸ��������ʿɵó��𰸣�
��2���������������BAC=90�����ABC=90�������ݵ���ֱ�������ε����ʼ�ȫ�������ε����ʿ������C�����ꣻ
��3������ͼ3������C��CL��y���ڵ�L����CL=1=BO������AAS��֤����BOE�ա�CLE���ó�BE=CE������ASA��֤����ABE�ա�BCF���ó�BE=CF������۵�֤��
����ͼ4������C��CK��ED�ڵ�K������C��CH��DF�ڵ�H������SAS��֤����CDE�ա�CDF���ɵá�BAE=��CBF���ɽ�ƽ���ߵ����ʿɵ�CK=CH=1��
��1����a24a+4+![]() ��0��
��0��
��(a2)2+![]() ��0��
��0��
�ߣ�a-2��2��0��![]() ��0��
��0��
��a-2=0��2b+2=0��
��a=2��b=-1��
��2���ɣ�1��֪a=2��b=-1��
��A��0��2����B��-1��0����
��OA=2��OB=1��
�ߡ�ABC��ֱ�������Σ��ҡ�ACB=45����
��ֻ�С�BAC=90�����ABC=90����
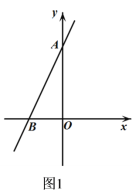
��������BAC=90��ʱ����ͼ1��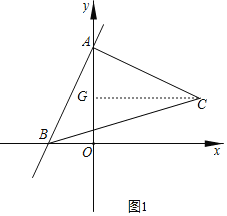
�ߡ�ACB=��ABC=45����
��AB=CB��
����C��CG��OA��G��
���CAG+��ACG=90����
�ߡ�BAO+��CAG=90����
���BAO=��ACG��
����AOB����BCP�� ��
��
���AOB�ա�CGA��AAS����
��CG=OA=2��AG=OB=1��
��OG=OA-AG=1��
��C��2��1����
��������ABC=90��ʱ����ͼ2��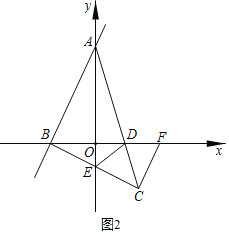
ͬ���ķ����ã�C��1��-1����
�������������ĵ�C��2��1����1��-1��
��3������ͼ3���ɣ�2��֪��C��1��-1����
����C��CL��y���ڵ�L����CL=1=BO��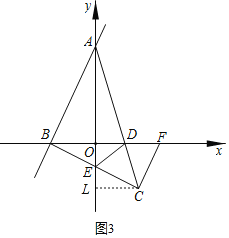
����BOE����CLE��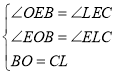 ��
��
���BOE�ա�CLE��AAS����
��BE=CE��
�ߡ�ABC=90����
���BAO+��BEA=90����
�ߡ�BOE=90����
���CBF+��BEA=90����
���BAE=��CBF��
����ABE����BCF�� ��
��
���ABE�ա�BCF��ASA����
��BE=CF��
��CF��![]() BC��
BC��
�ڵ�C��DE�ľ���Ϊ1��
��ͼ4������C��CK��ED�ڵ�K������C��CH��DF�ڵ�H��
�ɢ�֪BE=CF��
��BE=![]() BC��
BC��
��CE=CF��
�ߡ�ACB=45������BCF=90����
���ECD=��DCF��
��DC=DC��
���CDE�ա�CDF��SAS����
���BAE=��CBF��
��CK=CH=1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�