题目内容
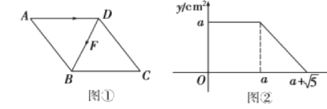
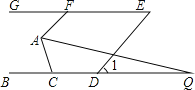
【题目】已知，如图AB∥DC，AF平分∠BAE，DF平分∠CDE，且∠AFD比∠AED的2倍小10°，则∠AED的度数为______．
【答案】76°
【解析】
过点F作FM∥AB，则有FM∥CD，，根据角平分线及平行线的性质，可得∠EAF=∠BAF=∠1，∠EDF=∠CDF=∠2，从而可得∠AFD=
(360°-∠E)，结合∠AFD=2∠E-10°即可求得结论.
过点F作FM∥AB，如图，
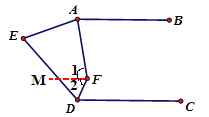
∵AB∥CD，
∴FM∥CD，
∵AF平分∠BAE，DF平分∠CDE，
∴∠EAF=∠BAF=∠1，∠EDF=∠CDF=∠2，
在四边形AEDF中，∠EAF+∠AFD+∠FDE+∠E=360°，
∴∠AFD=(360°-∠E)，
∵∠AFD=2∠E-10°，
∴(360°-∠E) =2∠E-10°，
解得，∠E=76°，
故答案为：76°.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某经销商从市场得知如下信息：
A品牌计算器 | B品牌计算器 | |
进价（元/台） | 700 | 100 |
售价（元/台） | 900 | 160 |
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台，设该经销商购进A品牌计算器x台，这两种品牌计算器全部销售完后获得利润为y元．
（1）求y与x之间的函数关系式；
（2）若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案？
（3）选择哪种进货方案，该经销商可获利最大？最大利润是多少元？
