题目内容
2、若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（ ）
分析：根据矩形的性质，得△AOB是等腰三角形，再由等腰三角形的性质进行答题．
解答：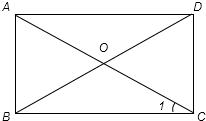
解：图形中∠1=40°，根据矩形的性质对角线相等且互相平分，则△AOB是等腰三角形，
∴∠OBC=∠1，则∠AOB=2∠1=80°．
故选C．
解：图形中∠1=40°，根据矩形的性质对角线相等且互相平分，则△AOB是等腰三角形，∴∠OBC=∠1，则∠AOB=2∠1=80°．
故选C．
点评：本题主要考查了矩形的性质，对角线相等且互相平分，矩形被对角线分成四个等腰三角形．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目