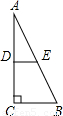题目内容
如图,有一等腰梯形纸片ABCD,AD∥BC,AB=CD,沿对角线AC将△ACD折叠,点D恰好落在BC边上的中点E处,则上底AD与对角线AC之间满足的等量关系应是 .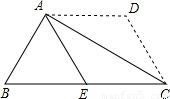
【答案】分析:由折叠的性质可得AD=AE,CD=CE,∠ECA=∠DCA,∠EAC=∠DAC,又由AD∥BC,易证得△AEC与△ADC是等腰三角形,即可得AE=EC=CD=AD,又由AB=CD,可得△ABE是等边三角形,继而求得△ABC是直角三角形,然后由三角函数的性质,即可求得上底AD与对角线AC之间的等量关系.
解答:解:根据折叠的性质:AD=AE,CD=CE,∠ECA=∠DCA,∠EAC=∠DAC,
∵AD∥BC,
∴∠DAC=∠ACE,
∴∠DAC=∠EAC=∠ECA=∠DCA,
∴AE=EC,AD=CD,
∴AE=EC=CD=AD,
∵E是BC边的中点,
∴BE=CE,
∵AB=CD,
∴AB=AE=BE=AD=CD,
∴∠B=∠BAE=∠AEB=60°,
∵∠AEB=∠EAC+∠ECA,
∴∠EAC=30°,
∴∠BAC=90°,
∴tan∠BCA=tan30°= =
=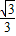 ,
,
∴AC=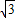 AB,
AB,
∴AC= AD.
AD.
故答案为:AC= AD.
AD.
点评:此题考查了等腰梯形的性质,等腰三角形的判定与性质,折叠的性质,以及直角三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用,注意特殊图形的性质.
解答:解:根据折叠的性质:AD=AE,CD=CE,∠ECA=∠DCA,∠EAC=∠DAC,
∵AD∥BC,
∴∠DAC=∠ACE,
∴∠DAC=∠EAC=∠ECA=∠DCA,
∴AE=EC,AD=CD,
∴AE=EC=CD=AD,
∵E是BC边的中点,
∴BE=CE,
∵AB=CD,
∴AB=AE=BE=AD=CD,
∴∠B=∠BAE=∠AEB=60°,
∵∠AEB=∠EAC+∠ECA,
∴∠EAC=30°,
∴∠BAC=90°,
∴tan∠BCA=tan30°=
 =
=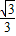 ,
,∴AC=
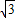 AB,
AB,∴AC=
 AD.
AD.故答案为:AC=
 AD.
AD.点评:此题考查了等腰梯形的性质,等腰三角形的判定与性质,折叠的性质,以及直角三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用,注意特殊图形的性质.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
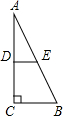 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一