题目内容
【题目】数学老师布置了这样一道作业题：
在△ABC中，AB=AC≠BC，点D和点A在直线BC的同侧，BD=BC，∠BAC=α，∠DBC=β，α+β=120°，连接AD，求∠ADB的度数．
小聪提供了研究这个问题的过程和思路：先从特殊问题开始研究，当α=90°，β=30°时（如图1），利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α=90°，β=30°以及等边三角形的相关知识便可解决这个问题．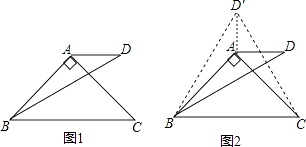
（1）请结合小聪研究问题的过程和思路，求出这种特殊情况下∠ADB的度数；
（2）结合小聪研究特殊问题的启发，请解决数学老师布置的这道作业题；
（3）解决完老师布置的这道作业题后，小聪进一步思考，当点D和点A在直线BC的异侧时，且∠ADB的度数与（1）中相同，则α，β满足的条件为（直接写出结果）．
【答案】
（1）
解：如图1
作∠AB D′=∠ABD，B D′=BD，连接CD′，AD′，
∵AB=AC，∠BAC=90°，
∴∠ABC=45°，
∵∠DBC=30°，
∴∠ABD=∠ABC﹣∠DBC=15°，
∵AB=AB，∠AB D′=∠ABD，B D′=BD，
∴△ABD≌△ABD′，
∴∠ABD=∠ABD′=15°，∠ADB=∠AD′B，
∴∠D′BC=∠ABD′+∠ABC=60°，
∵BD=BD′，BD=BC，
∴BD′=BC，
∴△D′BC是等边三角形，
∴D′B=D′C，∠BD′C=60°，
∵AB=AC，AD'=AD'，
∴△AD′B≌△AD′C，
∴∠AD′B=∠AD′C，
∴∠AD′B= 
∠BD′C=30°，
∴∠ADB=30°
（2）
解：第一种情况：当60°＜α≤120°时，
如图2，作∠AB D′=∠ABD，B D′=BD，连接CD′，AD′，
∵AB=AC，
∴∠ABC=∠ACB，
∵∠BAC=α，
∴∠ABC= 
=90°﹣ 
，
∴∠ABD=∠ABC﹣∠DBC=90°﹣ ﹣β，
同（1）可证△ABD≌△ABD′，
∴∠ABD=∠ABD′=90°﹣ ﹣β，BD=BD′，∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°﹣ 
=180°﹣（α+β），
∵α+β=120°，
∴∠D′BC=60°，
以下同（1）可求得∠ADB=30°，
第二种情况：当0°＜α＜60°时，
如图3，
作∠AB D′=∠ABD，B D′=BD，连接CD′，AD′．同理可得：∠ABC= 
，
∴∠ABD=∠DBC﹣∠ABC= 
，
同（1）可证△ABD≌△ABD′，
∴∠ABD=∠ABD′= ，BD=BD′，∠ADB=∠AD′B，
∴∠D′BC=∠ABC﹣∠ABD′=90°﹣ 
，
∴D′B=D′C，∠BD′C=60°．
同（1）可证△AD′B≌△AD′C，
∴∠AD′B=∠AD′C，
∵∠AD′B+∠AD′C+∠BD′C=360°，
∴∠ADB=∠AD′B=150°
（3）0°＜α＜120°，β=60°或120°＜α＜180°，0＜β＜60°时，α﹣β=120°或120°＜α＜180°，β=60°
【解析】解：（3）点D和点A在直线BC的异侧时，分三种情况讨论：
第一种情况：如图4，
当120°＜α＜180°，β=60°时，连接CD，
∵∠DBC=β=60°，BD=BC，
∴△DBC是等边三角形，
∴BD=CD，
∴△ABD≌△ACD，
∴∠ADB=∠ADC=30°，
第二种情况：如图5，
当120°＜α＜180°，0＜β＜60°时，连接CD′，
∠ABC= =90°﹣ ，
∠ABD=∠ABC+∠DBC=90°﹣ +β，
∵△ABD≌△ABD′，
∴∠ABD=∠ABD′=90°﹣ +β，
∵∠ADB=∠AD′B=30°，
∴∠BD′C=60°，
∵BD′=CD′，
∴△BD′C是等边三角形，
∴∠CBD′=（90°﹣ +β）+（90°﹣ ）=60°，
∴α﹣β=120°，
第三种情况：如图6，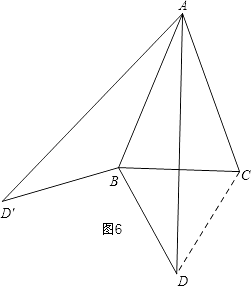
当0°＜α＜120°，β=60°时，连接CD，
与图4同理得：∠ADB=∠ADC=30°，
所以答案是：0°＜α＜120°，β=60°或120°＜α＜180°，0＜β＜60°时，α﹣β=120°或120°＜α＜180°，β=60°．
【考点精析】关于本题考查的全等三角形的性质，需要了解全等三角形的对应边相等; 全等三角形的对应角相等才能得出正确答案．
