题目内容
某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.| 时间(h) | 1 | 2 | 3 | 4 | … |
| 出水量(m3) | 2 | 4 | 6 | 8 | … |
(2)观察乙图,判断下列说法是否正确(对的打“√”,错的打“×”);
①0时到2时,两个进水口开放,出水口关闭;(√)
②2时到4时,出水口和两个进水口都开放或都关闭.(√)
(3)从4时起,同时打开出水口和一个进水口,何时刻该水池的蓄水量为2m3.
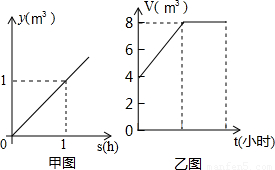
【答案】分析:(1)如图:当y=1时,x=1,故函数关系式为y=x.
(2)如乙图:在0到2时时,蓄水量上升,故是进水口开放,进水口关闭.
在2到4时,蓄水量保持不变,故表示出水量与进水量相平衡.都开放或关闭.
(3)由题意可知2x-x=8-2求得x=6,再加上原本的时间4时,即可知道10时水池蓄水量为2m3.
解答:解:(1)y=x (2分)
(2)①√;②√(6分)
(3)由题意,设x时水池蓄水量为2m3,得2x-x=8-2,(8分)
∴x=6.∴x+4=6+4=10.
答:10时水池蓄水量为2m3.(10分)
点评:本题考查一次函数的应用,考查从图象上获取信息的能力.
(2)如乙图:在0到2时时,蓄水量上升,故是进水口开放,进水口关闭.
在2到4时,蓄水量保持不变,故表示出水量与进水量相平衡.都开放或关闭.
(3)由题意可知2x-x=8-2求得x=6,再加上原本的时间4时,即可知道10时水池蓄水量为2m3.
解答:解:(1)y=x (2分)
(2)①√;②√(6分)
(3)由题意,设x时水池蓄水量为2m3,得2x-x=8-2,(8分)
∴x=6.∴x+4=6+4=10.
答:10时水池蓄水量为2m3.(10分)
点评:本题考查一次函数的应用,考查从图象上获取信息的能力.

练习册系列答案
相关题目
某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.
| 时间(h) | 1 | 2 | 3 | 4 | … |
| 出水量(m3) | 2 | 4 | 6 | 8 | … |
(2)观察乙图,判断下列说法是否正确(对的打“√”,错的打“×”);
①0时到2时,两个进水口开放,出水口关闭;(√)
②2时到4时,出水口和两个进水口都开放或都关闭.(√)
(3)从4时起,同时打开出水口和一个进水口,何时刻该水池的蓄水量为2m3.
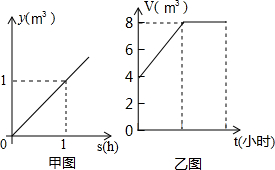
| 某个水池有2个进水口,1个出水口,每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示,某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示。 | ||||||||||||
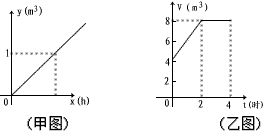 | ||||||||||||
| (1)观察甲图,写出每个进水口的进水量y(m3)与时间x(h)的函数关系式:_____; (2)观察乙图,判断下列说法是否正确(对的打“√”,错的打“×”); ①0时到2时,两个进水口开放,出水口关闭;( ) ②2时到4时,出水口和两个进水口都开放或都关闭。( ) (3)从4时起,同时打开出水口和一个进水口,何时刻该水池的蓄水量为2m3。 |
(2008•漳州)某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.
(1)观察甲图,写出每个进水口的进水量y(m3)与时间x(h)的函数关系式:______;
(2)观察乙图,判断下列说法是否正确(对的打“√”,错的打“×”);
①0时到2时,两个进水口开放,出水口关闭;(√)
②2时到4时,出水口和两个进水口都开放或都关闭.(√)
(3)从4时起,同时打开出水口和一个进水口,何时刻该水池的蓄水量为2m3.
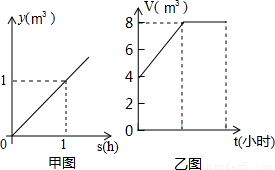
| 时间(h) | 1 | 2 | 3 | 4 | … |
| 出水量(m3) | 2 | 4 | 6 | 8 | … |
(2)观察乙图,判断下列说法是否正确(对的打“√”,错的打“×”);
①0时到2时,两个进水口开放,出水口关闭;(√)
②2时到4时,出水口和两个进水口都开放或都关闭.(√)
(3)从4时起,同时打开出水口和一个进水口,何时刻该水池的蓄水量为2m3.

 28、某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.
28、某个水池有2个进水口,1个出水口.每个进水口的进水量y(m3)与时间x(h)的关系如甲图所示,每个出水口的出水量(m3)与时间(h)的关系如下表所示.某天0到4时,该水池的蓄水量V(m3)与时间t(时)的关系如乙图所示.