题目内容
早晨小欣与妈妈同时从家里出发,小欣步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的路程(米)与时间(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回前往学校,若已知小欣步行的速度为50米/分钟,妈妈骑车速度为250米/分钟,并且妈妈与小欣同时到达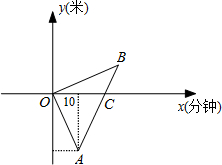 学校,完成下列问题:
学校,完成下列问题:
(1)求点A、点C的坐标;
(2)求过O、B两点的直线方程;
(3)求小欣早晨上学需要的时间.
 学校,完成下列问题:
学校,完成下列问题:(1)求点A、点C的坐标;
(2)求过O、B两点的直线方程;
(3)求小欣早晨上学需要的时间.
分析:(1)由直线的倾斜程度可知,OA代表妈妈行走的函数图象,且A的横坐标为10,求出此时对应的路程即为A的纵坐标的绝对值;而C点横坐标应该是小欣的妈妈从家到A然后又从A到家的时间;
(2)设直线OB的解析式为y=kx.由题意求出B的坐标,代入求出k的值即可;
(3)我们可根据小欣家到学校的距离来列方程,如果设小欣早晨上学用的时间为x分钟,那么他妈妈从C到B用的时间应该是x-20分钟,根据O-A段我们可计算出小欣妈妈的速度,然后根据小欣妈妈的速度×(x-20)=小欣的速度×x,列出方程,求出未知数.
(2)设直线OB的解析式为y=kx.由题意求出B的坐标,代入求出k的值即可;
(3)我们可根据小欣家到学校的距离来列方程,如果设小欣早晨上学用的时间为x分钟,那么他妈妈从C到B用的时间应该是x-20分钟,根据O-A段我们可计算出小欣妈妈的速度,然后根据小欣妈妈的速度×(x-20)=小欣的速度×x,列出方程,求出未知数.
解答:解:(1)∵妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回前往学校,妈妈骑车速度为250米/分钟,
∴此时妈妈行走的路程为:10×250=2500米,
∵A在第四象限,
∴点A的坐标为(10,-2500)
我们知道O-A用了10分钟,而A-C与O-A的路程相同,速度也相同因此AC段也该是10分种,因此C点的坐标应该是(20,0).
(2)设直线OB的解析式为y=kx.
∵当x=10时,10×50=500,
∴直线OB经过点(10,500),
∴500=10k,解得k=50.
∴直线OB的解析式为y=50x.
(3)由图象可知,点A的坐标为(10,-2500),说明妈妈骑车速度为250米/分钟,并返回到家的时间为20分钟.设小欣早晨上学时间为x分钟,则妈妈到家后在B处追到小欣的时间为(x-20)分钟,根据题意,得:50x=250(x-20),
解得:x=25,
答:小欣早晨上学时间为25分钟.
∴此时妈妈行走的路程为:10×250=2500米,
∵A在第四象限,
∴点A的坐标为(10,-2500)
我们知道O-A用了10分钟,而A-C与O-A的路程相同,速度也相同因此AC段也该是10分种,因此C点的坐标应该是(20,0).
(2)设直线OB的解析式为y=kx.
∵当x=10时,10×50=500,
∴直线OB经过点(10,500),
∴500=10k,解得k=50.
∴直线OB的解析式为y=50x.
(3)由图象可知,点A的坐标为(10,-2500),说明妈妈骑车速度为250米/分钟,并返回到家的时间为20分钟.设小欣早晨上学时间为x分钟,则妈妈到家后在B处追到小欣的时间为(x-20)分钟,根据题意,得:50x=250(x-20),
解得:x=25,
答:小欣早晨上学时间为25分钟.
点评:本题通过考查一次函数的应用来考查从图象上获取信息的能力.此类题是近年中考中的热点问题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
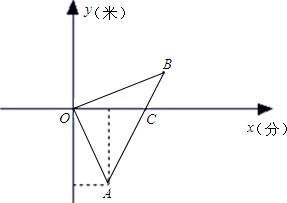 间x (分)的函数图象如图所示.已知A点坐标A(10,-2500),C(20,0)C点坐标为(20,0).
间x (分)的函数图象如图所示.已知A点坐标A(10,-2500),C(20,0)C点坐标为(20,0).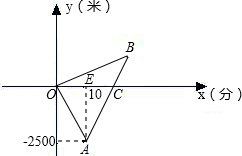 校.已知小欣步行速度为每分50米,求小欣家与学校距离及小欣早晨上学需要的时间.
校.已知小欣步行速度为每分50米,求小欣家与学校距离及小欣早晨上学需要的时间.
 时接到小欣的电话,立即以原来的速度返回并前往学校,若已知小欣步行的速度为50米/分钟,并且妈妈与小欣同时到达学校.完成下列问题:
时接到小欣的电话,立即以原来的速度返回并前往学校,若已知小欣步行的速度为50米/分钟,并且妈妈与小欣同时到达学校.完成下列问题: