题目内容
早晨小欣与妈妈同时从家里出发，步行与骑自行车到方向相反的两地上学与上班，图是他们离家的路程y（米）与时间x（分）的函数图象．妈妈骑车走了10分时接到小欣的电话，即以原速骑车前往小欣学校，并与小欣同时到达学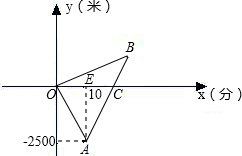
校．已知小欣步行速度为每分50米，求小欣家与学校距离及小欣早晨上学需要的时间．
分析：本题可有多种解法：方法一，根据小欣和妈妈到达学校的时间相同，列出等式进行求解即可；
方法二，根据待定系数法将直线OA与AB的函数关系式表式出来，两条直线的交点即为小欣家与学校的距离和小欣早晨上学所需的时间．
方法二，根据待定系数法将直线OA与AB的函数关系式表式出来，两条直线的交点即为小欣家与学校的距离和小欣早晨上学所需的时间．
解答：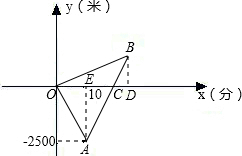
解：方法一：
由图象知，妈妈骑车的速度为2500÷10=250（米/分）．
设小欣家与学校距离为y米，
根据题意，得
=
+10
解得y=1250．
=25．
答：小欣家与学校距离为1250米，小欣早晨上学需要的时间为25分．
方法二：
设直线OB的解析式为y=kx．
∵当x=10时，10×50=500，
∴直线OB经过点（10，500），
∴500=10k，解得k=50．
∴直线OB的解析式为y=50x．
设直线AB的解析式为y=mx+b，
由题意知，C点坐标为（20，0）．
∵直线AB经过点A（10，-2500），C（20，0），
∴
．解得
．
∴y=250x-5000．
解方程组
得
．
答：小欣家与学校距离为1250米，小欣早晨上学需要的时间为25分．
解：方法一：由图象知，妈妈骑车的速度为2500÷10=250（米/分）．
设小欣家与学校距离为y米，
根据题意，得
| y |
| 50 |
| y+2500 |
| 250 |
解得y=1250．
| 1250 |
| 50 |
答：小欣家与学校距离为1250米，小欣早晨上学需要的时间为25分．
方法二：
设直线OB的解析式为y=kx．
∵当x=10时，10×50=500，
∴直线OB经过点（10，500），
∴500=10k，解得k=50．
∴直线OB的解析式为y=50x．
设直线AB的解析式为y=mx+b，
由题意知，C点坐标为（20，0）．
∵直线AB经过点A（10，-2500），C（20，0），
∴
|
|
∴y=250x-5000．
解方程组
|
|
答：小欣家与学校距离为1250米，小欣早晨上学需要的时间为25分．
点评：本题重点考查了一次函数图象和实际应用相结合的问题，可采用多种方法进行求解．
练习册系列答案
相关题目
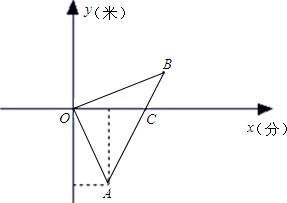间x （分）的函数图象如图所示．已知A点坐标A（10，-2500），C（20，0）C点坐标为（20，0）．
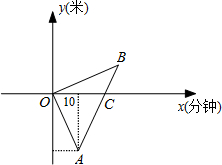学校，完成下列问题：
时接到小欣的电话，立即以原来的速度返回并前往学校，若已知小欣步行的速度为50米/分钟，并且妈妈与小欣同时到达学校．完成下列问题：