题目内容
半径为r的圆内接正三角形的边长为分析：根据题意画出图形，作出辅助线，利用垂径定理及勾股定理解答即可．
解答：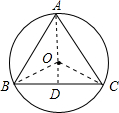
解：如图所示，OB=OA=r；
∵△ABC是正三角形，
由于正三角形的中心就是圆的圆心，
且正三角形三线合一，
所以BO是∠ABC的平分线；
∠OBD=60°×
=30°，
BD=r•cos30°=r•
；
根据垂径定理，BC=2×
r=
r．
解：如图所示，OB=OA=r；∵△ABC是正三角形，
由于正三角形的中心就是圆的圆心，
且正三角形三线合一，
所以BO是∠ABC的平分线；
∠OBD=60°×
| 1 |
| 2 |
BD=r•cos30°=r•
| ||
| 2 |
根据垂径定理，BC=2×
| ||
| 2 |
| 3 |
点评：本题考查学生对正多边形的概念掌握和计算的能力，解答这类题要明确，多边形的半径与外接圆的半径相同．
练习册系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形，则（ ）
| A、不能构成三角形 | B、这个三角形是等腰三角形 | C、这个三角形是直角三角形 | D、这个三角形是钝角三角形 |
半径为R的圆内接正三角形的面积是（ ）
A、
| ||||
| B、πR2 | ||||
C、
| ||||
D、
|