题目内容
【题目】如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD的中点，BF、ED的延长线交于点G，连接GC．
（1）求证：AB=GD；
（2）当CG=EG时，且AB=2，求CE．
【答案】（1）见解析；（2）CE=
.
【解析】
（1）根据三角形中位线定理得到DE∥AB，AB=2DE，根据平行线的性质得到∠ABF=∠DGF，证明△ABF≌△DGF，根据全等三角形的性质证明结论；
（2）证明△GEC∽△CBA，根据相似三角形的性质列出比例式，计算即可．
解：∵D，E是AC，BC的中点，
∴DE为△ABC的中位线，
∴DE∥AB，AB=2DE，
∴∠ABF=∠DGF，
∵F为AD中点，
∴AF=DF，
在△ABF和△DGF中，
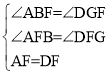
∴△ABF≌△DGF（AAS），
∴AB=GD；
（2）∵AB=2，
∴CD=2，DE=1，
∴GE=3，
∵CA=CB，
∴∠CAB=∠CBA，
∵CG=EG，
∴∠GEC=∠GCE，
∵DE∥AB，
∴∠GEC=∠CBA，
∴△GEC∽△CBA，
设CE=x，
则BC=2x，
∴
，即
，
解得：
，（负值舍去）
∴CE=.
练习册系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完．这两种节能灯的进价、售价如下表：
进价（元/只） | 售价（元/只） | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
（1）求幸福商场甲、乙两种节能灯各购进了多少只？
（2）全部售完100只节能灯后，商场共计获利多少元？
