题目内容
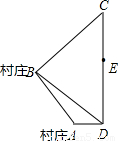
如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:方案一:E?D?A?B;
方案二:E?C?B?A.
经测量得AB=4
 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.

【答案】分析:(1)如图所示,过点B作BF⊥AD,交DA的延长线于点F.由于∠BDC=45°,∠ABD=15°,故利用三角形外角等于不相邻两个内角和知∠BAF=60°,即在直角三角形中,知道斜边求邻边用余弦得AF=ABcos60°=4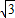 ×
× =2
=2 (千米),又BF=ABsin60°=4
(千米),又BF=ABsin60°=4 ×
×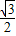 =6(千米)=DF所以可求出AD的值;
=6(千米)=DF所以可求出AD的值;
(2)过点B作BG⊥CD于G后,由矩形知BG=DF=6,由勾股定理知CG=8千米,有CD=CG+GD=14千米;
(3)由(2)得DE=CD-CE=8.方案一的铺设费用为:2(DE+AB)+4AD=40万元,方案二的铺设费用为:2(CE+BC+AB)=(32+8 )万元.故方案一的铺设电缆费用低.
)万元.故方案一的铺设电缆费用低.
解答:解:(1)过点B作BF⊥AD,交DA的延长线于点F.
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中, BF=ABsin60°=4
BF=ABsin60°=4 ×
×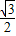 =6(千米),
=6(千米),
AF=ABcos60°=4 ×
× =2
=2 (千米).
(千米).
∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF-AF=6-2 (千米).
(千米).
即河宽AD为(6-2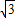 )千米;
)千米;
(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中, =8(千米),
=8(千米),
∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD-CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8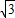 )万元.
)万元.
∵40<32+8 ,
,
∴方案一的铺设电缆费用低.
点评:解此题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,利用三角函数的知识,进行解答即可.
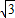 ×
× =2
=2 (千米),又BF=ABsin60°=4
(千米),又BF=ABsin60°=4 ×
×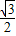 =6(千米)=DF所以可求出AD的值;
=6(千米)=DF所以可求出AD的值;(2)过点B作BG⊥CD于G后,由矩形知BG=DF=6,由勾股定理知CG=8千米,有CD=CG+GD=14千米;
(3)由(2)得DE=CD-CE=8.方案一的铺设费用为:2(DE+AB)+4AD=40万元,方案二的铺设费用为:2(CE+BC+AB)=(32+8
 )万元.故方案一的铺设电缆费用低.
)万元.故方案一的铺设电缆费用低.解答:解:(1)过点B作BF⊥AD,交DA的延长线于点F.
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中,
 BF=ABsin60°=4
BF=ABsin60°=4 ×
×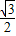 =6(千米),
=6(千米),AF=ABcos60°=4
 ×
× =2
=2 (千米).
(千米).∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF-AF=6-2
 (千米).
(千米).即河宽AD为(6-2
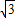 )千米;
)千米;(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中,
 =8(千米),
=8(千米),∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD-CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8
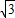 )万元.
)万元.∵40<32+8
 ,
,∴方案一的铺设电缆费用低.
点评:解此题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,利用三角函数的知识,进行解答即可.

练习册系列答案
相关题目
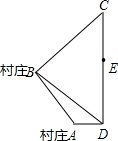 如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案: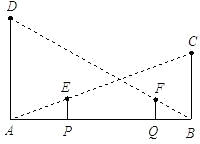 6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.
6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.
 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.