题目内容
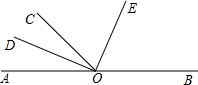 如图,O是直线AB上的一点,OD平分∠AOC,OE平分∠BOC.则∠DOE的度数α是
如图,O是直线AB上的一点,OD平分∠AOC,OE平分∠BOC.则∠DOE的度数α是
- A.90°<α<180°
- B.0°<α<90°
- C.α=90°
- D.α随折痕BC位置的变化而变化
C
分析:由于OD是∠AOC的平分线,OE是∠COB的平分线,所以∠AOD=∠COD,∠COE=∠BOE,所以∠DOE的度数α是平角度数的一半.
解答:∵OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠DOC= ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC,
∴∠DOE= ∠AOC+
∠AOC+ ∠BOC=
∠BOC= ∠AOB,
∠AOB,
又∵点O是直线AB上的点,
∴∠DOE= ∠AOB=90°,即α=90°.
∠AOB=90°,即α=90°.
故选C.
点评:考查了角平分线的定义和角的计算,解决角的运算类问题时,充分利用已知条件和隐含条件(平角、余角、补角、对顶角等)是解题的关键.
分析:由于OD是∠AOC的平分线,OE是∠COB的平分线,所以∠AOD=∠COD,∠COE=∠BOE,所以∠DOE的度数α是平角度数的一半.
解答:∵OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠DOC=
 ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC,∴∠DOE=
 ∠AOC+
∠AOC+ ∠BOC=
∠BOC= ∠AOB,
∠AOB,又∵点O是直线AB上的点,
∴∠DOE=
 ∠AOB=90°,即α=90°.
∠AOB=90°,即α=90°.故选C.
点评:考查了角平分线的定义和角的计算,解决角的运算类问题时,充分利用已知条件和隐含条件(平角、余角、补角、对顶角等)是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
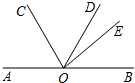 如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.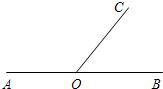
 如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数.
如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数.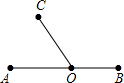 如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是
如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是 如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题:
如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题: